
| SDSS Classic |
| SDSS.org |
| SDSS4.org |
| SDSS3.org |
| SDSS Data |
| DR19 |
| DR17 |
| DR10 |
| DR7 |
| Science |
| Press Releases |
| Education |
| Image Gallery |
| Legacy Survey |
| SEGUE |
| Supernova Survey |
| Collaboration |
| Publications |
| Contact Us |
| Search |

| Observing Operations | Reviews | Survey Management |
Scientific Requirements and Scientific Commissioning for the SDSS
Michael A. Strauss, Princeton University
Contents
1 Introduction
This document outlines the top-level scientific requirements of the Sloan Digital Sky Survey, and describes how these requirements can be tested and monitored during the scientific commissioning and operations. For each requirement, its scientific basis is given (and whenever appropriate, a reference is given as well). The tests that need to be carried out during scientific commissioning to confirm that these requirements are met are outlined. The continuing tests that can be done on the data to confirm that these requirements are met are also described (this is an aspect of quality assurance). The emphasis everywhere is on requirements that can be confirmed with well-defined tests with relatively small quantities of data; without this emphasis, it will be impossible to carry out the commissioning in a finite amount of time.There already exist a number of documents, mostly on the Web, laying down requirements for various aspects of the survey. The present document is largely based on the requirements that have been laid down previously. There is a web page, which includes links to these various previous documents (as well as the present document). Every attempt has been made not to contradict previously adopted requirements.
In particular, there already exists a comprehensive requirements document for SDSS software.
In addition, there exists a number of documents which have been written about the test year itself; they can be found from the test year page. In particular, see the latest version of the test year plan (although this document needs work). This document has much overlapping content with the present document, but sorts things in a somewhat orthogonal way.
After summarizing the parameters of the survey, this document systematically goes through each of the major areas of quantitative requirements. For each, it outlines the following:
- 1.
- The quantitative requirements themselves. For most of the sections below, there are several distinct numbered requirements.
- 2.
- The scientific justification for the requirement.
- 3.
- The consequences of not meeting the requirement; that is, what our fallback position should be if we find we are not meeting it, or what scientific goals we would not be able to reach.
- 4.
- The tests we must do during the scientific commissioning to convince ourselves that we are meeting the requirement, including both the data that need to be obtained, and the analyses to be done with these data. This is really the incorporation of the test year plans into the present document.
- 5.
- Who has been given the authority to carry out these tests, and who has been given authority to sign off on them. Generically, this authority is given to the Science Commissioning Committee (SCC), which reports directly to the Project Scientist, the Director for Program Management, and the Project Director. We have indicated individuals throughout who have these responsibilities at the time that this was written; this perhaps should be replaced with their titles, so that the document stays valid if individual's jobs change.
- 6.
- The timescale within which these tasks will be done.
- 7.
- The resources required to carry out these tasks.
- 8.
- Quality Assurance; how we can confirm that these requirements continue to be met during routine operations. Data that don't do so will be declared not to be of survey quality.
- 9.
- Enhanced goals, as appropriate.
- 10.
- Further test year tasks. For any given area, it is likely that there will be test year tasks that cannot be explicitly expressed in terms of quantitative requirements. This may include pieces of software that can only be written with real data in hand, or scientific analyses needed by the pipeline to set relevant parameters. Then would follow a breakdown, as above, of what data are needed, what analysis is needed, who is responsible, what the timescale is, and how we know when we're done.
- 11.
- What's missing; a to-do list for the requirements document itself.
- 12.
- Eventually, this document could be augmented with reports of progress on each of the tests being carried out, and indications of when we have confirmed that a given requirement is met.
Note that not every one of the above items is included for every requirement.
In its present form, this document is not complete; I've indicated in various sections where further work needs to be done. Many of the individual sections have been written in collaboration with various individuals in the SDSS; their names are indicated.
2 Science Goals of the Survey
The basic science goals of the SDSS are outlined in the SDSS Principles of Operation (PoO). They are as follows:- 1.
- To perform a CCD imaging survey of roughly
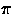 steradians in
image quality of
steradians in
image quality of 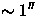 FWHM for point sources in the
Northern Galactic hemisphere in 5 bands to u'=22.3, g'= 23.3, r'=23.1,
i'=22.3, z'=20.8 (5
FWHM for point sources in the
Northern Galactic hemisphere in 5 bands to u'=22.3, g'= 23.3, r'=23.1,
i'=22.3, z'=20.8 (5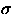 limit for point sources).
limit for point sources).
- 2.
- To perform a CCD imaging survey in the equatorial stripe in the Southern Galactic hemisphere in 5 bands, roughly 200 square degrees, to roughly two magnitudes fainter.
- 3.
- To obtain high quality spectra and thus redshifts for a set of 106 galaxies and 105 quasars carefully chosen from the imaging data.
- 4.
- To provide the data in a form to enable state-of-the-art studies of the large-scale distribution of galaxies and quasars, the luminosity function of quasars for 0 < z < 5, and the properties and evolution of galaxies, and to identify and study galaxy clusters.
- 5.
- To finish the survey in a span of roughly 5 years.
Although there are myriad other scientific products which the SDSS will produce, they are either secondary to the above (e.g., Galactic structure studies) or are necessary intermediate steps for carrying out the above (e.g., the reddening map); they are described below, where appropriate.
More details, and specifications of the hardware, may be found in the Appendix.
3 Image Quality and Throughput
This section was written together with Jim Gunn.
The depth of the imaging scans is determined by the aperture of
the telescope, the scan rate, the size of the CCD's, the transmission
of the atmosphere, the sky brightness, the reflectivity
of all relevant optics, the quantum efficiency and
noise properties of the CCD detectors, the
seeing and image quality, and the efficacy of the
reduction software. The Black Book estimates the effect of all these
quantities, and finds that the 5
![]() detection limit for a point source in 1'' seeing should be
u' = 22.3, g' = 23.3, r' = 23.1, i' = 22.3, and z' = 20.8. See
§ A.4 for a brief summary of the design parameters
of the imaging camera.
detection limit for a point source in 1'' seeing should be
u' = 22.3, g' = 23.3, r' = 23.1, i' = 22.3, and z' = 20.8. See
§ A.4 for a brief summary of the design parameters
of the imaging camera.
3.1 Quantitative Requirements
We put requirements only on the parts of the system that we have control over with the as-built telescope and instrument. These requirements are drawn from the requirement documents for the telescope and for the camera; see the Appendix.
- 1.
- Image Quality on the Imaging Chips
- (a)
- The telescope in scanning mode off the equator should return images with better than 1.1'' Full-Width-Half-Maximum (FWHM) in 0.8'' FWHM free-air seeing. The design with perfect optics and 0.8'' free-air seeing returns images over the field with FWHMs between 0.83'' and 1.04'', with images over 1'' only at the extreme edges of the field in u' and z'. With optical surface quality corresponding to 0.3'' RMS image errors, we should easily be able to meet the 1.1'' requirement, and to better it over most of the field.
- (b)
- The variation in the FWHM of the PSF over the CCD imaging array should be less than 30% in 0.8'' free-air seeing, and the variation over a single chip should be less than 15%. The optical design yields a maximum variation of FWHM over a given detector of 12% with 0.8'' free-air seeing, in the edge z' chip, which also has the worst images. It also yields a variation of the FWHM across the array of 25%.
- (c)
- During routine operations, the ellipticity of the PSF should be less than 12% on all chips. The design yields a maximum ellipticity when the array is in perfect focus of 7%, though in the edge fields this is very highly focus-dependent, and rises in some cases to 14% with the focus off by only 100 microns (18 microns on the secondary). Might this be affected by differential chromatic refraction in the u' and g' chips at high airmass?
- (d)
- After correction for the power-law scattering wings, the energy circle enclosing 90% of the received energy should have a radius less than 2.5 arcseconds. When the design images are convolved with a double-Gaussian fit to a 0.8'' Kolmogorov seeing profile, the circle enclosing 50% of the energy is in all cases within a few hundredths of an arcsecond (4%) of the FWHM. The 90% encircled energy circle is in all cases between 2.0 and 2.2 arcseconds. In the real images, this diameter is strongly influenced by the power-law scattering wings, which typically contain between 5% and 10% of the energy, roughly an order of magnitude more than is predicted by diffraction. The scattering wings can be subtracted in software, and we require that the 90% circle be smaller than 2.5 arcseconds once this is done.
- 2.
- CCD read-noise: The read-noise of the photometric chips should be below 10 e- (u') and 20 e- (g'r'i'z').
- 3.
- Signal-to-Noise Ratio: The system should reach signal-to-noise 50 for point sources in 1'' seeing at magnitudes no brighter than 18.9, 20.5, 20.2, 19.6, and 18.1 in the five bands, and reach the detection signal-to-noise limit of 5 at 21.9, 23.2, 22.8, 22.2, and 20.7, both under photometric conditions at airmass 1.4 and with free-air seeing of 0.8 arcsecond. These brightness levels are uniformly 0.2 magnitude brighter than expected theoretically. Note that this puts an (indirect) requirement on sky brightness.
- 4.
- Throughput and Quantum Efficiency: A 20.0 magnitude star scanned at sidereal rate with the photometric chips at an airmass of 1.4 under photometric conditions should give more than 1300, 9000, 9000, 6500, and 1500 e-, for the five filters, respectively. These values are 75% of those expected theoretically with the typical measured QE of the CCDs. This may be thought of as a necessary condition to meet the previous requirement.
- 5.
- Further requirements COULD be written down on ghosting, bad columns, scattered light, CTE, full well, and so on. One could write down what is expected here, but there is little that could be done if requirements are not met. One expects appreciable ghosts a priori only in u' and z'; one sees appreciable ghosts only in u'.
- 6.
- J. Gunn will write requirements on the performance of the astrometric chips.
- 7.
- Seeing: The worst images over the photometric array for acceptable imaging data should have a FWHM no worse than 1.2''.
- 8.
- Completeness of the Imaging Coverage: No more than 3% of frames, averaged over 1/2 hour of scanning, may be rejected for non-astronomical reasons (bad seeing, airplane trails, focus problems, etc.) before the scan in question is marked for reobservation.
3.2 Scientific Justification
Obtaining deep CCD imaging of the surveyed area is one of the basic scientific goals of the SDSS. This requires high throughput and good image quality. This drives the number of objects detected, the efficiency of star-galaxy separation at all magnitudes, the signal-to-noise ratio of the images of spectroscopic targets, and so on. Good seeing clearly pushes all these requirements in the same direction.The median free-air seeing at the site is believed to be 0.8''; with the above requirements, one can image on roughly 1/2 of the dark photometric nights. ``Photometric nights'' are defined in the following section.
Roughly 3% of the sky will be masked due to bright stars; the completeness of the imaging coverage allows an equal amount of sky missed for non-astronomical reasons.
3.3 Consequences of Not Meeting Requirements
Star-galaxy separation, measures of image shape, and the depth of the data will all be strongly affected.- 1.
- The image quality is measured for each chip by the on-line Data Acquisition system.
- 2.
- The image quality is measured for each chip by the Postage Stamp Pipeline (PSP).
- 3.
- The read-noise on each photometric chip has been measured; all are known to meet the requirements.
- 4.
- The Differential Image Motion Monitor will allow us to measure the free-air seeing directly, so as to test the image quality requirements.
- 5.
- We can determine the real signal-to-noise ratio at a given flux level from multiple observations of a given region of sky.
- 6.
- The throughput of each chip is determined by the Photometric Telescope operations. Mamoru Doi's calibration system will also be available for measurements of the throughput of the camera itself.
- 7.
- Image quality can be assessed with the PSP once data are taken while tracking along great circles.
3.4 How do we determine if these requirements are met?
3.5 Who's in Charge?
- 1.
- These requirements are on both the telescope and imaging camera, so Gunn is responsible for tuning the hardware to meet these requirements.
- 2.
- The tests to confirm that the requirements are met can be found in diagnostic plots created by the PSP. It is the responsibility of the pipeline developers and production system people at Princeton and Fermilab to examine the results.
3.6 Estimated timescale for confirming these requirements
Fall 1999. By this point, the integration of the PT and imaging camera data, the final collimation of the optics, and the telescope drive system, will all be complete.3.7 Quality Assurance
- 1.
- The PSP and astroline/IOP will have diagnostics which can be used to indicate when the PSF becomes unacceptable.
- 2.
- The PSP will continually measure the throughput of the camera/telescope, given the calibration from the PT.
- 3.
- There must be Quality Assurance tools on the mountain to tell the observers in close to real time when the PSF becomes unacceptable. There must be Quality Assurance tools following the running of the photometric pipeline that flag data as unacceptable due to poor PSF, poor signal-to-noise ratio, or poor throughput.
- 4.
- Mamoru Doi's calibration system can be used to measure the throughput, readnoise, and the gain of all the cameras on the chips.
3.8 What's Missing
- 1.
- We need requirements on the accuracy and efficiency of the outputs of the photometric pipeline (and the errors given for each quantity), especially quantities used in target selection, such as Petrosian magnitudes. See § 6 and the software requirements document for some of this.
- 2.
- We need a requirement on the completeness of the photometric sample as a function of magnitude (separately for stars and galaxies).
4 Photometric Uniformity and Accuracy
This section has been written by Steve Kent and Michael Strauss.The photometric calibration of the SDSS data is accomplished by obtaining accurate photometry of stars in numerous ``secondary patches'' with the Photometric Telescope, which are subsequently scanned by the 2.5m. The full calibration process is a multi-step procedure, and the allowable errors from each step are detailed below. The error budget here is quite tight, and it is realized that not all these items will be realizable at the start of the survey, and as we learn more, the calibrations may be tightened. For example, after several years, one can use the multiple observations of the primary standards to improve the definition of the photometric system, and thus improve the photometric accuracy further. This is called out explicitly in what follows.
All errors given are rms unless otherwise indicated.
4.1 Quantitative Requirements
The systematic rms errors in calibrating the 2.5m data to the SDSS photometric system after two years of routine operation should be
- Magnitudes: < 0.02 mag rms over the sky in r' band.
- Colors: < 0.02 mag rms in (g'-r'), (r'-i'), and < 0.03 mag in (u'-g'), (i'-z'), for objects with colors bluer than those of an M0 dwarf (i.e., u'-g' = 2.7; g'-r' = 1.2; r'-i' = 0.6; i' - z' = 0.4, from Lenz et al. (1998), ApJS, 119, 121).
Magnitudes and colors are computed for any random sample of objects bright enough that photon shot noise is negligible, over the whole sky. At the beginning of the survey, these numbers should be 0.03 mag in magnitudes and g'-r', r'-i', and 0.04 mag in u'-g', i'-z'.
Note: the values of the errors in magnitudes and colors are the same; this allows for the fact that often there are correlated errors in the raw magnitudes which partially cancel when computing colors.
The 2% (or 0.02 mag) allowed error in the r' magnitude and colors as defined above
has 11 contributions; the error from each contribution is arbitrarily
taken to be ![]() , although ultimately it is the
combination of all ten that must be constrained. For a few of these
contributions, we use a smaller error, where it is justified. We list the error
budget here; the final two items are end-to-end tests.
, although ultimately it is the
combination of all ten that must be constrained. For a few of these
contributions, we use a smaller error, where it is justified. We list the error
budget here; the final two items are end-to-end tests.
- 1.
- Primary standard star calibration - internal error.
- (a)
- Requirement: The uncertainty in the mean magnitude and r' color for each primary star should be no more than 1% relative to a system defined by any group of > 10 stars.
- (b)
- Basis: We use 10 stars to define 3 constants (a, b, k)
in a typical photometric solution; the system is defined to
an accuracy
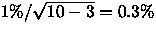 . So this item has a
smaller contribution to the error budget than do the other
contributions.
. So this item has a
smaller contribution to the error budget than do the other
contributions.
- (c)
- How to test:
- Compute rms residuals for a primary standard relative to the mean from observations over one year, and from this, compute errors in the mean.
- (d)
- Who is in charge: Alan Uomoto
- 2.
- Primary standard star calibration - external error.
- (a)
- Requirement: The transformation from the USNO 40'' to the PT instrumental systems should add no more than 0.6% random error to the photometric system, per star.
- (b)
- Basis: We use USNO to set up the standard star system, but will use the PT to calibrate the 2.5m. The photometric systems of the two are not identical.
- (c)
- How to test:
- Obtain parallel calibration of the full set of primary standards with the MT, the PT, and the USNO 40'', and confirm that they are on the same system. Compute residuals as a function of color, magnitude, and Right Ascension, and look for trends.
- (d)
- Who is in charge: Alan Uomoto
- 3.
- PT Linearity.
- (a)
- Requirement: Uncorrected nonlinearities due to imperfect shutter timing and nonlinear CCD/amplifier gain in the PT shall be less than 0.3%, measured as the peak error between shortest and longest exposure times, and between the faintest and brightest unsaturated stars.
- (b)
- Basis: The primary standard stars are observed with short integrations at high count rate, while secondary patches are observed with longer integrations at low count rate. Any nonlinearities will give systematic errors in the secondary patch calibration. A peak error is more relevant than rms error.
- (c)
- How to test:
- i.
- Carry out laboratory tests of linearity using a calibrated light source.
- ii.
- Carry out laboratory tests of shutter shadowing using a stable light source. Compare results of shortest and longest exposure times, and measure variation in the throughput across the CCD.
- iii.
- Observe primary standards at a variety of exposure times, and compare results as a function of exposure time.
- (d)
- Who is in charge: Alan Uomoto
- 4.
- Nightly PT extinction and zero-point determination.
- (a)
- Requirement: The uncertainty of the best-fit solution to the primary star magnitudes determined over a 1.5 hour interval should be less than 0.6% in all bands, for airmasses between 1 and 1.75, not including the uncertainty in the primary star magnitudes themselves. That is, the scatter of the standard stars around the best-fit solution, divided by the square root of the number of degrees of freedom, should be less than 0.6%, after correcting for the known uncertainty of the primary star magnitudes.
- (b)
- Basis: This test accounts for errors from uncorrected variations in extinction during a night and any other uncalibrated effects. Airmass 1.75 is the highest airmass at which survey scans will be taken. Note that it does not include the effects of uncertainties in the standard star magnitudes themselves; that is covered in the first two items above.
- (c)
- How to test:
- i.
- Carry out observations of the primary standards only within a small area on the PT CCD, so as to minimize the effects of flatfield variations (see next item below). Compute the residuals of each star from the global photometric solution on each night. Compute the mean and standard deviation of the residuals over ten or more nights, and correct for contributions from errors in the standard star calibrations.
- ii.
- Observe twenty or more primary standards with the PT on one night. Divide observations into two groups randomly, by time, and by azimuth. Apply the photometric solution derived from one group to the other, and compare with the known values. Repeat for 10 nights.
- iii.
- Further tests defined by Alan Uomoto.
- (d)
- Who is in charge: Alan Uomoto
- 5.
- Flatfielding of PT CCD patches.
- (a)
- Requirement: The rms variation in photometric calibration of any star measured in different positions of the PT CCD shall be no worse than 0.6%.
- (b)
- Basis: Standard stars are observed in a small area of the CCD, while secondary stars in the patches cover the entire area. About 1/3 the area of the PT CCD is used in calibrating any 2.5m scanline. The true error in the flatfield over this region is NOT averaged out. It is possible that we can do substantially better on this item.
- (c)
- How to test:
- i.
- Expose a single star in a
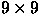 grid over the PT CCD. Compute
the rms variation in the calibrated magnitude relative to
the mean.
grid over the PT CCD. Compute
the rms variation in the calibrated magnitude relative to
the mean.
- ii.
- Obtain PT frames of secondary fields spaced by one-half the CCD width. Compute the mean difference in the calibration in overlap regions.
- (d)
- Who is in charge: Alan Uomoto
- 6.
- Calibration of PT patches.
- (a)
- Requirement: The zeropoint for photometry of faint PT stars anywhere in a secondary patch shall have an rms error no worse than 0.6% relative to the mean zero-point for bright stars in the patch. This error includes sky subtraction and any algorithmic systematic errors, but excludes flatfielding errors and photon statistics. It is presumed that these contributions to this error are systematic and thus do not cancel out for many stars in a patch. Here
- (b)
- Basis: Sky subtraction and aperture corrections are important potential sources of error for faint stars. The dividing line between bright and faint assumed here is a tunable parameter in MTpipe; we use this definition consistently throughout this section. But we might consider ``bright'' to refer to stars bright enough that photon statistics in their photometry is negligible, while ``faint'' are the majority of objects at relatively low signal-to-noise value, which will be used for the calibration of the secondary patches.
- (c)
- How to test.
- i.
- For a few patches, measure a field with lots of bright stars repeatedly, moving the field by 1/2 CCD between exposures. (This test overlaps the flatfielding test above). Compare the average difference in calibrations between the exposures for the bright and faint stars in the field, respectively.
- ii.
- In overlaps between the PT patches and 2.5m imaging fields, compare the calibration zero points between bright and faint stars. That is, look at the solution for the aperture correction as a function of magnitude.
- (d)
- Who is in charge: Alan Uomoto and Doug Tucker
- 7.
- Photometric mismatch between PT and 2.5m CCDs after applying
a linear color term.
- (a)
- Requirement: The rms photometric mismatch between the PT and 2.5m imaging camera shall be no worse than 0.6% for main sequence stars of spectral type between O5 to M0.
- (b)
- Basis: This requirement is just a placeholder to make sure that the mismatch is actually quantified.
- (c)
- How to test: It can be calculated by direct computation, given the known CCD and filter responses, and the SED's of stars.
- (d)
- Who is in charge: Alan Uomoto
- 8.
- Variations in aperture correction within a single 2.5m CCD.
- (a)
- Requirement: The photometric pipeline aperture correction shall have an internal rms error no bigger than 0.6% averaged over column number for arbitrary camera column, filter, and seeing between 0.8 and 1.5 arcsec.
- (b)
- Basis: The aperture correction converts PSF counts to the counts inside a large aperture. Because of PSF variations, this quantity will vary across a CCD field. The photometric pipeline will take this variation into account as best it can. We may be able to do substantially better than this requirement.
- (c)
- How to test:
- i.
- Compute the aperture correction on an individual basis for isolated bright stars. Compute the rms residuals relative to those actually used by the photometric pipeline, over the full range of columns and for 3 fields spanning a PT patch, and look for trends with column number.
- (d)
- Who is in charge: Steve Kent and Robert Lupton
- 9.
- Spatial variation in photometric calibration within a single 2.5m CCD.
- (a)
- Requirement: The rms variation in the zeropoint difference between PT stars and 2.5m stars evaluated over the full range of columns in each 2.5m chip shall be no worse than 0.6% within a single PT patch, for seeing between 0.8 and 1.5 arcsec.
- (b)
- Basis: The photometric calibration is affected by scattered light in the telescope; this manifests itself as a dependence of the zeropoint on column number. The scattered light pattern may vary with telescope and rotator orientation. We may be able to do substantially better than this requirement.
- (c)
- How to test:
- i.
- Compute the rms difference of the 2.5m and PT magnitude as a function of column number for bright stars. Use aperture magnitudes for the 2.5m measurements, to avoid possible problems with PSF variations across the chip.
- ii.
- Repeat this exercise for faint stars at a Galactic latitude which has enough stars to beat the photon noise per star in the PT measurements. This allows us to confirm that the bright and faint stars are on the same photometric system.
- iii.
- Repeat the above with the telescope at a range of rotator orientations and elevations.
- (d)
- Who is in charge: Steve Kent
- 10.
- Time variation of the aperture correction along a stripe:
- (a)
- Requirement: The photometric pipeline aperture correction for each chip shall have an rms error no bigger than 0.6% averaged over one hour, for arbitrary camera column, filter, and seeing between 0.8 and 1.5 arcsec.
- (b)
- Basis: Changes in seeing and focus can cause cause variations
in the PSF and hence aperture corrections; errors in the
latter translate directly into photometric errors. The
photometric transfer from a calibration patch to an arbitrary
point in a 2.5m scan includes a term ``apCorr(point) -
apCorr(patch)''; the rms error of this term is
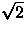 times the rms error at a single point.
times the rms error at a single point.
- (c)
- How to test:
- Compute the aperture correction on an individual basis for isolated bright stars. Compute the rms residuals relative to those actually used by the photometric pipeline, over the full range of columns and for 3 fields spanning a PT patch, and look for trends with row number.
- (d)
- Who is in charge: Steve Kent
- 11.
- Time variation of photometricity along a stripe:
- (a)
- Requirement: The rms variation in the photometric zero-point shall not exceed 0.6% over an arbitrary time span for any camera column.
- (b)
- Basis: This test is an end-to-end test of the transfer of calibration from the PT to the 2.5m; additional errors may come from atmospheric extinction variations and other uncalibrated sources.
- (c)
- How to test:
- Observe PT patches overlapping 2.5m scans with 1/2 hour separation. PT patches shall have been measured in close proximity in time and reduced in a single excal run with one extinction coefficient. Compute the rms of extinction-corrected zero points. Use data with minimal change in seeing to eliminate it as a variable. Use big aperture magnitudes on the 2.5m data to eliminate the effect of variable PSF.
- (d)
- Who is in charge: Steve Kent
These next requirement is not independent of the above; rather, it combines a number of the requirements just listed.
- 12.
- Additional end-end test
- (a)
- Requirement: The rms variation in multiple detections of the same bright object (for which shot noise is negligible) in independent scans shall not exceed 2.4%.
- (b)
- Basis: This test is an end-to-end test of the PT to 2.5m transfer, and tests the internal consistency of calibrations. However, it is largely immune to external errors in the primary standard star calibration, nonlinearities in the PT, and photometric mismatch between the PT and 2.5m.
- (c)
- How to test:
- i.
- Obtain a single 2.5m scan perpendicular to the main survey stripe pattern. Compute rms difference for objects detected in common. The figure 2.4% presumes that errors between different scans are statistically independent (which is almost but not quite true).
- ii.
- A less complete test is simply to compare results for several observations of a given scan, in the same direction.
- (d)
- Who is in charge: Steve Kent
4.2 Scientific Justification
The requirements above are driven by the science goals outlined here.- 1.
- Science of large scale structure from the galaxy and quasar
redshift surveys shall not
be significantly affected by photometric errors (including the effects
of Galactic extinction). Errors in
photometric zero point cause errors in galaxy counts that
mimic large scale structure in any apparent magnitude limited sample.
On angular scales comparable to that of the whole survey, an error
budget to the galaxy number counts in the
spectroscopic survey is roughly as follows:
- (a)
- 2% True large-scale structure
- (b)
- <4% Uncorrected Galactic extinction
- (c)
- 1% Uncorrected errors in completeness corrections
- (d)
- 2% Systematic photometric error.
- 2.
- For quasar target selection:
- (a)
- Photometric errors shall not contribute appreciably to the number of false negatives. Those quasars which have colors that put them close to the stellar locus will not be observed spectroscopically. Systematic errors in photometry cause the region in color-color space that is omitted to wander relative to the locus of all quasars, making the selection of quasar targets non-uniform. It is required that the variation in incompleteness and types of quasars that are selected be small. The error is TBD.
- (b)
- Photometric errors shall not contribute appreciably to the
number of false positives.
Systematic errors in photometry cause the measured stellar locus to wander relative to the fixed selection criteria, increasing the number of stars falsely identified as quasars. Similarly, statistical errors in photometry cause the stellar locus to broaden, scattering stars into the region of color-color space occupied by quasars. This is particularly important at
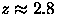 , where the quasar locus
passes particularly close to that of stars.
, where the quasar locus
passes particularly close to that of stars.
The intrinsic rms width of the stellar locus in color space is 0.04 mag at its fattest. We wish that this increase by no more than 10% to keep the quasar false positives to a minimum. If we presume Gaussian errors, then the maximum tolerable increase in observational error (per color projected perpendicular to the stellar locus) is
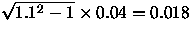 mag. This then can be taken as the acceptable error in g'-r'
and r'-i'. The u'-g' error can be twice as large.
mag. This then can be taken as the acceptable error in g'-r'
and r'-i'. The u'-g' error can be twice as large.
Stars redder than M0 have a larger intrinsic cosmic scatter in their colors than do bluer stars; also, their spectra are complex and cause the linear relationships used in the color terms in the photometric calibrations to break down. Loosening the requirements on photometric accuracy for these red objects is not likely to compromise science.
References:
- i.
- Notes by S. Kent presented at Oct 1992 SAC meeting.
- ii.
- Don Schneider, private communication
- iii.
- Heidi Newberg, private communication. Report for Simulation \#3
4.3 Consequences of Not Meeting Requirements
Systematic magnitude errors will strongly affect the large-scale structure core-science goals of the SDSS. Random magnitude errors, if they are quantified, can be taken into account in large-scale structure studies. Both systematic and random color errors strongly affect the completeness, efficiency, and uniformity of the quasar survey, with a deleterious effect on the quasar science goals.
4.4 Who is in Charge?
Alan Uomoto has overall responsibility to verify that the outputs of Photometric Telescope are correct. Steve Kent is in charge of end-to-end quality, due to multiple people involved in different sets of tests. See above for specific responsibility for specific tests.4.5 Quality Assurance
Quality assurance will be conducted in multiple places:- 1.
- Online monitoring: A set of frames in one filter will be analyzed on the PT DA computer to determine a quick, rough zero point during the night. This information is not used in data processing, but will allow the observers to determine whether a given night is photometric.
- 2.
- MT pipeline diagnostics. The major diagnostics are the residual errors in the photometric solutions (which provide a measure of internal error in the solution) and comparison of calibration constants with expected values. The first can be used to reject a night outright and is equivalent to test (4) in §4.1 above; the second diagnostic can be used as a warning.
- 3.
- Photo pipeline diagnostics include test (9) from above, which monitors problems with 2.5m flatfielding, and the change in the position and width of the stellar locus with field number, which tests item (10) above, and can be used as a warning diagnostic.
- 4.
- Final calibration diagnostics include test (9) from above, and comparison of calibration constants with expected values. The first test can be used to detect flatfielding problems and reject a run.
- 5.
- Database diagnostics: The principal diagnostic is a test of photometric repeatability for objects detected in overlap regions of the different scanlines and stripes. The test largely repeats test (12) above, although it does not fairly test (8) and (9). The rms differences should not exceed 3.6%.
4.6 What's Missing
- We need to flesh out the requirements on reddening and QSOs better. This will improve as we gain experience with testing the color selection criteria for QSOs from actual spectroscopy. The following is a possible statement of the requirement on reddening:
- The interstellar reddening should be determined, with a maximum rms error in colors of 1.5%. This yields rms errors in r' extinction, as determined from stellar colors, of order 3%.
5 Astrometric Requirements
Requirements on astrometry fall into two categories: requirements on absolute astrometry in a given band (we refer here to r'), and requirements on the relative astrometry between bands. We treat the two separately here. This section of the document was prepared by Jeff Pier, based in part on the minutes of a meeting to discuss astrometric requirements. For background information giving the history of astrometry requirements, see this document.Each requirement in this section is expressed as an rms figure per coordinate in units of milli-arcseconds (hereinafter mas) along a great circle.
5.1 Requirements on Absolute Astrometry
5.1.1 Quantitative Requirements
The requirements in this subsection apply to the positions determined in r' for point-source objects brighter than r' = 19 with spectral type between O5 and M0. The determination of positions for very blue, very red, or emission-line objects may, and certainly occasionally will, fail to meet the requirements, due to differential chromatic refraction.
It is expected that the requirements herein will be satisfied for each
``acceptable imaging run.'' Here an acceptable imaging run is a scan of
length no less than 20 minutes (exclusive of ``ramp-up'' frames),
airmass ![]() ,seeing
,seeing ![]() '' (FWHM), with the absolute telescope pointing error
no worse than 3 arcsec rms (2-D on the sky) and relative telescope
tracking error no worse than 50 mas (1-D on the sky) on time scales
of 1-10 minutes.
'' (FWHM), with the absolute telescope pointing error
no worse than 3 arcsec rms (2-D on the sky) and relative telescope
tracking error no worse than 50 mas (1-D on the sky) on time scales
of 1-10 minutes.
There are three different levels of requirement for absolute astrometry:
- 1.
- The ``Drop-Dead'' requirement - if the astrometry does not meet this, the run will be deemed unacceptable since core survey science would be jeopardized: The absolute astrometry on the sky should be no worse than 180 mas.
- 2.
- The ``Science Goals'' requirement - the astrometry should routinely
meet this requirement to enable non-core science:
The absolute astrometry on the sky should be no worse than 100 mas.
- 3.
- The ``Enhanced Goal'' requirement - if all goes well (i.e.,
the telescope tracks well, the atmosphere (seeing, anomalous refraction)
are favorable, the catalog density is at or above 10 stars/deg2) the
astrometry should be limited by the atmosphere:
Reasonable effort should be expended to attain absolute astrometry on the sky of 60 mas. (N.B. - the number that appears here is really no more than an educated guess about the properties of the atmosphere.)
5.1.2 Scientific Justification
- 1.
- The requirement of 180 mas ensures that astrometric errors do not contribute significantly to loss of spectroscopic fiber throughput (see the ``Black Book,'' Section 10.1, as well as the requirements on drilling accuracy).
- 2.
- Currently (and soon to be) available all-sky/wide-area astrometric catalogs can be used with SDSS data to determine proper motions. The 100 mas requirement ensures that the accuracy of the proper motion determinations will be limited by the other catalogs, not by SDSS. Additionally, SDSS data will be used to identify optical counterparts of objects detected in other spectral regions. Again, this requirement will ensure that SDSS positions are not the limiting factor in making the identifications.
- 3.
- There is no specific scientific justification for the enhanced goal.
Rather it is felt that the survey astrometry should be ``as good as it
can be.'' The astrometric performance can be no better than limits imposed by
- (a)
- the effects of the atmosphere (``seeing'' and ``anomalous refraction'');
- (b)
- discontinuous telescope motions due, for example, to glitches in tracking or in mirror motion;
- (c)
- the accuracy and density of available astrometric reference frames (catalogs).
5.1.3 Consequences of Not Meeting Requirements
If the ``Drop-Dead'' requirement is not met it will seriously impact the core science of the Survey; the signal-to-noise ratio of the spectra will be degraded. If the ``Science Goals'' requirement is not met, the SDSS astrometry will dominate the error budget in future proper motion studies.5.1.4 How do we determine if these requirements are met?
The ideal, direct way to determine astrometric performance is simply to compare star positions determined with SDSS with those determined externally. Since positions of objects in the r' photometric bandpass are required, it is necessary to compare positions of stars which are fainter than 14th magnitude (and indeed down to 19th to fully satisfy the requirement). The only wide-area astrometric catalogs available for such comparisons with accuracies reliably better than our requirement of 180 mas are the catalogs constructed from the POSS-II plates (catalogs of the northern sky are being generated by the USNO's PMM machine, STScI's digital sky survey and Minnesota's Automated Plate Scanner). These catalogs are expected to be accurate to about 150 mas at the epoch at which they were taken.
The equatorial
astrometric zones established by USNO for SDSS can be used to judge
performance to higher accuracy. These
zones have typical astrometric accuracies of 70 mas at the faint
end (![]() ). These fields are limited to the equator and
do not allow for a full exploration of telescope tracking parameter
space, and offer only a limited range for exploring atmospheric
variations across the sky. They do represent, however, our best
external check on astrometric performance.
). These fields are limited to the equator and
do not allow for a full exploration of telescope tracking parameter
space, and offer only a limited range for exploring atmospheric
variations across the sky. They do represent, however, our best
external check on astrometric performance.
For the future, the USNO is conducting a ``red lens survey'' which will reach to about 16th magnitude with an accuracy approaching 50 mas. The southern red lens survey is underway now and should finish in the year 2000, after which the telescope/detector will be moved to the northern hemisphere. Once operational, it will require an additional two years to complete the observations. While the catalog produced from this survey may be helpful in eventually producing an astrometric catalog over the SDSS survey area, it will not be available to help determine the SDSS performance in the first few years of the survey.
But, for now, the alternative is to use a boot-strap approach: matching detections on the astrometric chips with catalog positions of astrometric reference stars, then transferring the solution, using bridge stars of intermediate magnitudes, to the r' bandpass. (This is, in fact, how the astrometry solution is done in the first place.) This method is somewhat circular but is really the only choice.
It is difficult to perform external checks to accuracies better than 150 mas or so since SDSS is in the happy position of being unique as an astrometrically accurate, wide-area, faint-limit survey.
Repeated scans of the same patch of sky will allow for a very useful
consistency/internal check, but such experiments will not be able to
rule out all systematic effects. The number of secondary overlap stars can
be enlarged by scanning a strip once, then scanning again after shifting
the bore-sight by half a chip-width (instead of the normal ![]() chip-width) for consistency checking. Another possibility is to scan
over a given region in different directions. For example, we could
carry out a few scans in a direction perpendicular to the main scans,
which should have quite different systematics.
chip-width) for consistency checking. Another possibility is to scan
over a given region in different directions. For example, we could
carry out a few scans in a direction perpendicular to the main scans,
which should have quite different systematics.
5.1.5 Quality Assurance
The following QA will be generated by the Astrometric Pipeline, for use by Survey Operations to reject or accept the Pipeline run:- 1.
- For each CCD separately, the ensemble mean and rms residuals in both great circle longitude and latitude from the least-squares fit are calculated. Separate values will be generated for the entire scan, and for each segment of the scan, where the length of the segment is set in the test year by the expected number of standard stars per segment. A warning is issued if the mean or rms for any segment, or for the scan as a whole, exceeds a fiducial value.
- 2.
- For each CCD separately, the number of standard stars matched and used in the least-squares fit within each segment is tabulated. A warning is issued if the number of stars for any segment is less than a fiducial value.
- 3.
- A measure of the goodness-of-fit for the least-squares fit is
calculated. Whether
this is a
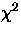 value, a run-up-test, or some other value is yet to
be determined. A warning is issued if this value exceeds a fiducial value.
This is not yet implemented.
value, a run-up-test, or some other value is yet to
be determined. A warning is issued if this value exceeds a fiducial value.
This is not yet implemented.
- 4.
- A given standard star will typically be detected 2 to 4 times on the astrometric chips in a single imaging run. These are matched in the pipeline, and their positions averaged. Matching is performed between the leading and trailing astrometric chips in each column, and between adjacent columns (using the positions averaged over the two astrometric chips in each column). The ensemble mean and rms residuals (in catalog mean place) are calculated in both great circle longitude and latitude for each match-up (6 leading/trailing match-ups, 10 adjacent column match-ups). Separate values will be generated for the entire scan, and for each segment of the scan. A warning is issued if the mean or rms exceeds a fiducial value.
- 5.
- The change in the zero-order terms for the CCD and dewar offsets, rotations, and scale factors, relative to the input values from the ``opCamera" file are tabulated. A warning is issued if any values differ from their fiducial values by more than an acceptable error.
- 6.
- Information regarding the tracking performance of the telescope can be generated from the fitted focal plane model (e.g., maximum deviation of the bore-sight perpendicular to the desired tracking path). This information would not be used to judge the performance of the pipeline. However, if any quantity exceeded a fiducial value, a warning could be issued so that the mountain could be informed of a potential problem.
- 7.
- There is no code in IOP to compare results from the leading and trailing chips, but it would be useful for these purposes.
5.1.6 Who's in Charge
The U.S. Naval Observatory has responsibility for astrometric performance. The team leader is Jeff Pier. Responsibility for telescope mechanical and optical performance lies with the telescope engineering group, French Leger is the leader. The effort for work on telescope tracking and pointing is led by Paul Czarapata. Responsibility for atmospheric phenomena is beyond the scope of this document.3.8 Further Test Year Tasks
The astrometric test year plans can be found off the astrometric pipeline's homepage here.There is also a related set of engineering/acceptance tests to be performed on the telescope here.
There is an extensive list of requirements/specifications for telescope and telescope tracking performance here.
Deducing the relative contributions to astrometric error from (1) the atmosphere, (2) telescope, (3) camera, and (4) astrom pipeline+catalogs is a non-trivial matter. Here are a few suggestions:
- 1.
- Run simulated data through the pipeline: if the simulations are correct(!!), one should be able to gauge the pipeline performance, since one knows the input parameters, including complicating factors arising from hardware and/or the atmosphere put into the simulations. This kind of testing has been carried out in the past, and with correct inputs from the simulation, the pipeline returns errors which are consistent with the input parameters.
- 2.
- Carry out multiple observations of a given region of sky (both with the telescope parked on the equator, and scanning in great circles) and compare the astrometric results. Any differences cannot be due to problems in the input catalogs.
- 3.
- On several windless nights with excellent seeing, park the telescope on the equator and scan: the resulting errors should be due to the atmosphere or catalog systematics or pipeline problems. The difficulty here is ascertaining that nothing is moving (i.e. no movements of telescope optics, telescope axes, wind baffle, camera, no focus changes, no LN2 fillings, or anything else one can think of).
5.1.8 What's Missing
The astrometric test year plans need to be incorporated into this document, and the specific quantitative goals by which we can say that the system passes each test need to be spelled out.It would also be useful to work out a full error budget for astrometric accuracy, in the style of § 4.
5.2 Relative Astrometry Between Bands
5.2.1 Quantitative Requirements
The requirements of this subsection are described here. As in the absolute astrometry requirements, there are three levels of requirement. Relative astrometry is measured not on an object-by-object basis, but is averaged over timescales of a frame or perhaps somewhat longer (to be determined). As with the absolute astrometry goals, these are understood to apply to objects of ``normal'' colors with r' < 19.- 1.
- The ``Drop-Dead'' requirement - if the relative astrometry does not meet this, the run will be deemed unacceptable since core survey science would be jeopardized: The relative astrometry between adjacent colors should be no worse than 180 mas on the timescale over which the relative astrometry is determined.
- 2.
- The ``Science Goals'' requirement - the relative astrometry should routinely
meet this requirement to enable non-core science:
The relative astrometry between adjacent colors should be no worse than 100 mas.
- 3.
- The ``Enhanced Goal'' requirement.
Reasonable effort should be expended to attain relative astrometry between adjacent colors of 40 mas.
5.2.2 Scientific Justification
- 1.
- Relative astrometry of 180 mas is adequate for merging of objects, and is acceptable for deblending.
- 2.
- Relative astrometry of 100 mas is ideal for deblending, and also minimizes systematic errors in aperture photometry colors.
- 3.
- Relative astrometry of 40 mas allows Kuiper Belt objects to be recognized due to their parallax between the images of different colors of a given frame.
5.2.3 Consequences of Not Meeting Requirements
If the drop-dead goal is not met, the deblender will have to be run with much looser constraints on distinguishing close blends, with strong consequences for studies of close pairs of objects, and rejection of moving objects (asteroids).5.2.4 How do we determine if these requirements are met?
The photometric pipeline delivers the mean offset between frames (now done only to Level 0), and the error thereof. Question: Are these quantities which will be stored in the database? This quantity is used as quality assurance as well.5.2.5 Who's in Charge
As with the absolute astrometric requirements, the U.S. Naval Observatory has responsibility for this requirement as well. The input of the photometric pipeline, in the form of Robert Lupton and Zeljko Ivezic, is relevant.5.1.7 Further Test Year Tasks
We need to determine whether a single frame is the optimal timescale to measure the mean astrometric offset between frames, given the nature of the atmosphere. If it is longer, the calculation cannot be done within frames, and it will have to be rethought. However, it is probably true that in this case, we can go ahead with the current code within the astrometric pipeline for determining the relative offsets between colors; this probably meets the drop-dead requirement already.6 Target Selection
This section has been written by David Weinberg and Michael Strauss.The ``target selection requirements'' in effect impose requirements on the data reduction pipelines (photo in particular), the target selection pipeline, and the target selection algorithms, given the properties of data returned by the telescope/camera/spectrographs under survey imaging conditions. The primary ``adjustables'' are the algorithms themselves and the definitions of acceptable observing conditions for survey imaging and spectroscopy.
The primary requirement is that spectroscopic target selection be uniform enough that uncertainties in the selection function will not be the limiting factor in studies of galaxy clustering, quasar clustering, or distribution functions (such as the luminosity function) of the galaxy and quasar populations. However, a requirement worded in this form is essentially impossible to check prior to completing and analyzing the SDSS. We therefore list quantitative, testable requirements below with the hope that meeting these requirements will also mean meeting this underlying requirement. A secondary desideratum for the target selection algorithms is that they select a broad range of galaxy and quasar types. In other words, the main galaxy and quasar samples should be as ``complete'' as possible to a given apparent magnitude limit, to the extent that this completeness can be accomplished without compromising the uniformity of the samples or being too inefficient.
The sample selection listed below will involve ``fuzzy'' boundaries. For example, close to the nominal photometric limit of the galaxy or quasar sample, the probability that an object is chosen is not a step-function of magnitude, but rather a slowly varying function. This gives target selection some robustness to errors in the photometry, and allows exploration of the sample selection near the sample boundaries.
The three main science samples are:
- 1.
- A selection of galaxies to a magnitude limit in
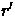 , with
an additional cut on surface brightness to ensure high spectroscopic
completeness. The current plan is to use Petrosian magnitudes and half-light
surface brightness as the selection parameters, with auxiliary
selection with fiber magnitudes.
, with
an additional cut on surface brightness to ensure high spectroscopic
completeness. The current plan is to use Petrosian magnitudes and half-light
surface brightness as the selection parameters, with auxiliary
selection with fiber magnitudes.
- 2.
- An auxiliary selection of galaxies determined by photometric redshifts to be particularly luminous and red, going approximately 1.5 magnitudes fainter in r' than the main galaxy sample.
- 3.
- A selection of quasars based on their optical colors,
apparent magnitudes, and 20 cm radio fluxes (from the FIRST survey). For the
purposes of this discussion, a
quasar is defined as any extragalactic object whose optical light is
dominated by an unresolved core with at least one of the following
properties:
- (a)
- A non-stellar continuum;
- (b)
- Strong, broad (FWHM>500 km s-1) emission lines; or
- (c)
- Strong high-ionization emission lines.
The current descriptions of these algorithms are given in ``Galaxy and Cluster Selection Algorithm for SDSS'', and ``Quasar Target Selection Algorithm''; many further explications and analyses can be found via the galaxy and quasar working group mailing lists. Algorithms should not be constrained by coding convenience; it is fair to say that the target selection algorithms are as important as those in upstream pipelines.
For brevity, we will refer to the objects in the main galaxy sample as ``galaxies'' and to those in the auxiliary sample as ``BRGs'' (for bright red galaxies). Note that calibration targets (e.g., spectrophotometric standards) are not explicitly mentioned here, nor are stellar and serendipitous science targets; these do not belong in the high-level requirements document. Also not described here are requirements on interactions between targeted objects. See Steve Kent's software requirements document for these and other details.
The targets selected for the Southern strip survey will be a superset of those selected by these algorithms -- e.g., with more generous magnitude limits, surface brightness cuts, color cuts, and morphology cuts.
Once targets are selected based on the pipeline outputs in the operational database, they are assigned to spectroscopic tiles. Some fraction of the tiled targets will be lost because they lie within 55" of another target.
6.1 Quantitative Requirements
- 1.
- Surface Density of Galaxies: The mean surface density of galaxy and BRG targets, averaged over a (not necessarily contiguous) region of 50 square degrees or larger, will be in the range 90-110 per square degree.
- 2.
- Redshift Success of Galaxies: At least 95% of galaxy targets (main sample) will yield a measurable, reproducible redshift, and will indeed be determined to be a galaxy (and not a star at z = 0) under standard spectroscopic observing conditions. The fraction of galaxy targets which yield a redshift on one spectroscopic exposure under standard conditions, and not another, must be well-characterized.
- 3.
- Completeness of Galaxy Target Selection: In regions of the sky that are not masked (due to bright stars, etc.), 95% of galaxies whose true magnitude and surface brightness are both at least 0.2 mag (mag/arcsec2 for surface brightness) above the selection thresholds will be selected. No more than 5% of galaxies whose true magnitude and surface brightness are both at least 0.2 mag below the selection thresholds will be selected. In between these limits, the dependence of selection probability on true magnitude and surface brightness will be reasonably smooth.
- 4.
- Reproducibility of Galaxy Target Selection over Range
of Observing Conditions:
Consider two photometric scans covering a given
15 square degree region spanning
the range of acceptable survey imaging conditions; let Pi,k be
the selection probability assigned to galaxy i in run k, and Nk
be the total number of galaxies selected in run k. Target
selection must be robust (although fuzzy), thus
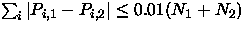 .
.
- 5.
- Uniformity of Galaxy Target Selection: Patches of size
15 square degrees at different Galactic and survey latitude and
longitude will yield surface densities of galaxy spectroscopic targets
that are the same to within 50%. Surface densities rather than
raw numbers are specified because the fraction of sky that is masked
may depend on stellar density. The fluctuations given are still a
place-holder; intrinsic fluctuations on this scale due to large-scale
structure are thought to be of order 15% rms, so the above value may
be a guess of the relevant peak-to-peak variations.
BRGs:
- 6.
- Redshift Success of BRGs: At least 85% of BRG targets in the main sample will yield a measured, reproducible redshift under standard spectroscopic observing conditions. The fraction of BRG targets which yield a redshift on one spectroscopic exposure under standard conditions, and not another, must be well-characterized.
- 7.
- Completeness of BRG Target Selection: In regions of the sky that are not masked (due to bright stars, etc.), 95% of BRGs whose true (absolute magnitude, rest frame color) are (0.2, 0.1) above the selection thresholds will be selected. No more than 5% of BRGs whose true (absolute magnitude, rest frame color) are (0.2,0.1) below the selection thresholds will be selected. In between these limits, the dependence of selection probability on true magnitude and surface brightness will be reasonably smooth.
- 8.
- Reproducibility of BRG Target Selection over Range
of Observing Conditions: Consider two photometric scans covering a
15 square degree region spanning
the range of acceptable survey imaging conditions. Let Pi,k be
the selection probability assigned to BRG i in run k, and Nk
be the total number of BRGs selected in run k. Target
selection must be robust (although fuzzy), thus
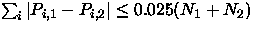 .Quasars:
.Quasars:
- 9.
- Surface Density of Quasars: The mean surface density of quasar candidates in the cap region averaged over a region of 15 square degrees or larger, will be 20 per square degree. The mean surface density of quasar targets in the skirt region will be 8 per square degree. The density of high-redshift quasar candidates also needs to be set.
- 10.
- Quasar Target Selection Efficiency: At least 65% of z < 5 quasar targets in the cap region will be true quasars (i.e., not stars, or non-AGN galaxies) that yield a measured, reproducible redshift under standard spectroscopic observing conditions. The corresponding minimum fraction for quasar targets in the skirt region will be 40%.
- 11.
- Quasar Selection Completeness: In a region of sky reasonably well sampled by existing quasar surveys in the literature, the quasar target selection should successfully select 90% of all known quasars in the region brighter than i' = 19.
- 12.
- Reproducibility of Quasar Target Selection over Range
of Observing Conditions: Consider two photometric scans covering a
15 square degree region spanning
the range of acceptable survey imaging conditions. Let Pi,k be
the selection probability assigned to quasar i in run k, and Nk
be the total number of quasars selected in run k. Target
selection must be robust (although fuzzy), thus
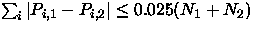 .Miscellaneous:
.Miscellaneous:
- 13.
- Covering of the Tiling Algorithm: The tiling algorithm will fail to tile no more than 10-2 of the selected galaxy and quasar targets. This was first written down as 10-3, which is almost certainly unattainable at reasonable cost. We have to be especially careful near the edges of a tiled region.
- 14.
- Robustness to Photometric Errors: The target selection of galaxies, BRG's, and quasars, should be robust to known photometric errors.
6.2 Scientific Justification
As mentioned in the introduction to this section, the main scientific justification underlying all of these requirements is that our measurements of the clustering and distribution functions of the galaxy and quasar populations should not be limited by uncertainties in the selection function. A second general justification, especially relevant for quasars and to some extent BRGs, is to identify objects for follow-up studies. For example, we would like to identify a high fraction of the bright quasars (i'<18) as targets for follow-up high-resolution spectroscopy. Justifications for the specific quantitative requirements are given below, labeled according to the requirement numbers above.
- 1.
- This surface density gives 106 galaxies over 104 square degrees. The sky coverage and error reflect our understanding of the fluctuations due to large-scale structure.
- 2.
- The 95% threshold ensures that we will get close to our desired goal of 106 galaxies, with small contribution from stars selected incorrectly as galaxies. From the point of view of sample uniformity, the essential requirement is that the targets that do not yield redshifts do so for reasons that are independent of the spectroscopic observing conditions (e.g., they have no useful spectroscopic features within our bandpass), so that the selection function is simply multiplied by a constant redshift incompleteness factor. We clearly need to characterize the variation of the fraction of objects for which we are unable to measure redshifts, as this variation will leave an imprint on large-scale structure measures.
- 3.
- This is the main requirement ensuring uniformity of the galaxy sample for large scale structure and galaxy population studies. In order to determine the selection function, we need to be able to compute for each sample galaxy the maximum distance to which it would be included in the sample (or, more generally, the probability of inclusion as a function of distance). This is only possible if the galaxies that should be included are included and the galaxies that should be excluded are excluded. Note that this wording allows fuzzy selection boundaries to be implemented. Note also that this and the following two requirements ask for consistency in the star-galaxy separation to the spectroscopic limit.
- 4.
- This is a secondary requirement aimed at ensuring uniformity of the galaxy sample, again allowing fuzzy boundaries. It implies that the properties of the selected galaxies do not depend significantly on the imaging conditions. This then puts important requirements on the robustness of the galaxy photometry, and the star-galaxy separation. These may well be the principal determination of the maximum acceptable seeing, transparency, and sky brightness for the survey.
- 5.
- This is a third requirement aimed at ensuring uniformity of the galaxy sample, concentrating on effects that could produce fluctuations in the efficiency of target selection on angular scales comparable to that of the survey itself. Potential effects of this sort include influence of bright stars on sky subtraction, errors in the a priori extinction map or the photometric calibration, or hardware effects that depend on the direction in which the telescope is pointing. The requirement is fairly weak as worded, due to the substantial contribution from large-scale structure on these scales.
- 6-8.
- The requirements and justifications are analogous to those of [2-4] for the main galaxy sample. The numbers are looser because the questions we aim to address with the BRG sample are less detailed, and because it seems unrealistic to think that we can obtain the same level of spectroscopic completeness for the BRG sample as for the main galaxy sample (if we can, we are perhaps being too conservative in our apparent magnitude limit).
- 9.
- With the default numbers above, we would get 80,000 quasars in the 5,000 square degree cap if the selection efficiency in this region is 80%, and 20,000 quasars in the 5,000 square degree skirt if the selection efficiency in this region is 50%; however, the minimum efficiency numbers listed in [10] are below this.
- 10.
- The combination of this with requirement [9] determines the number of quasars that will actually be discovered by the SDSS.
- 11.
- We would like to have as complete a quasar sample as possible within the limits of practicality, so that studies of the quasar population are not limited by selection biases. We would ideally like to have had an absolute requirement on the completeness of quasar target selection, but such a requirement would necessarily be untestable without a spectroscopic survey of every stellar object over a quite large area. As known quasars have been selected with a wide range of techniques, this requirement captures the spirit of the ideal requirement.
- 12.
- This ensures uniformity of the quasar sample, especially important for clustering measurements.
- 13.
- The galaxies that are missed because they are not tiled will
have a complicated spatial pattern that depends on details of tiling
algorithm and the observing strategy. It will be virtually impossible
to correct measures of large scale structure for this effect because
it will be so poorly understood, so we adopt a conservative limit on
the fraction of galaxies that can be missed. Of course a much larger
fraction of galaxies (
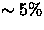 ) will be missed because of the
minimum fiber spacing, but this is an effect that is easy to understand
and can be compensated for in a straightforward manner. Note that we
have not written down an equivalent requirement on tiling
efficiency; the tiling algorithm gives a one-to-one correspondence
between efficiency and completeness, and the requirement on the
timescale of the survey require that tiling be conducted at high
efficiency.
) will be missed because of the
minimum fiber spacing, but this is an effect that is easy to understand
and can be compensated for in a straightforward manner. Note that we
have not written down an equivalent requirement on tiling
efficiency; the tiling algorithm gives a one-to-one correspondence
between efficiency and completeness, and the requirement on the
timescale of the survey require that tiling be conducted at high
efficiency.
- 14.
- This requirement suggests fuzzy boundaries on magnitude cuts, as described above. Moreover, as discussed in § 4, the photometric errors are likely to be larger at the beginning of the survey than in the end; target selection should take this into account, and allow enough fuzziness that a complete sample can be defined from the spectroscopic data once improved photometry is available.
6.3 Consequences of Not Meeting Requirements
As above, these numbers refer to item numbers in the quantitative requirements subsection.- 1.
- Either the final sample does not contain the desired number of galaxies or the survey takes longer to complete.
- 2.
- The final sample contains substantially fewer galaxies than originally intended, and/or the main galaxy sample is non-uniform in a way that is difficult to quantify because of its dependence on observing conditions.
- 3.
- The selection function of the main galaxy sample is uncertain because the maximum distance at which a galaxy would make it into the sample is poorly known.
- 4.
- The selection function of the main galaxy sample is uncertain because the number and properties of the selected galaxies depend on observing conditions.
- 5.
- The selection function of the main galaxy sample has coherent fluctuations that may prevent successful measurement of large scale structure on scales comparable to the survey. Failure to meet this requirement might also indicate a problem that would affect other aspects of survey science, including those based on BRGs and quasars.
- 6-8.
- Analogous to [3-5], for the BRG sample.
- 9.
- Either the final sample does not contain the desired number of quasars or the survey takes longer to complete.
- 10.
- The final sample does not contain the desired number of quasars (note interaction with [9]).
- 11.
- The quasar sample is missing scientifically interesting classes of quasars, reducing its usefulness for studies of the quasar population and for identifying targets for follow-up studies.
- 12.
- The quasar sample is non-uniform in a way that depends on observing conditions, limiting the precision of quasar clustering measurements.
- 13.
- Measurements of large scale galaxy clustering are uncertain because of the unknown influence of tiling incompleteness.
- 14.
- There may be gradients in the target selection samples as a function of time, as the photometry gradually improves.
6.4 How do we determine if these requirements are met?
- 1,9.
- After imaging multiple areas, we tune the selection thresholds (primarily the magnitude limit) in order to get the desired surface densities. Note that for quasars this will require imaging at a range of Galactic positions and appropriate averaging, since the density of candidates will vary with stellar density even though the density of quasars should not. We need to determine how many such areas are needed.
- 2.
- Using spectroscopic observations, including multiple observations of several fields over the full range (and presumably beyond the full range) of acceptable survey spectroscopy conditions. We would also imagine loosening the galaxy target selection criteria, especially on surface brightness, to see to what low surface brightness we might be able to go. This would allow us to do large-scale structure studies as a function of surface brightness. One could carry out a long series of 15 minute spectroscopic exposures of a sample of galaxies extending several tenths of a magnitude fainter than the nominal limit, and ask how many needed to be co-added to meet the redshift completeness requirement at each magnitude.
- 3.
- This the most important of the requirements, at least from the point
of view of galaxy large scale structure studies, and it is also the toughest
to check because in general we do not know the ``true'' values of galaxy
photometric parameters. There are two useful methods for assessing
whether this requirement is being met:
- (a)
- Photometric parameters measured from a 1/4 sidereal, hence deep
imaging scan are taken as ``truth,'' since they are measured at higher
signal-to-noise ratio (although such a test does not check all
systematic effects). This test requires a deep scan of a significant
area of sky (probably
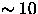 square degrees, yielding
square degrees, yielding 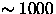 galaxy
targets, although the exact value remains to be determined) followed
by one or more scans of the standard depth.
Alternatively, we can co-add multiple frames (or, much easier, the
atlas images) taken of a given region of sky
scanned at sidereal rate; this requires that the code to co-add atlas
images must be developed.
galaxy
targets, although the exact value remains to be determined) followed
by one or more scans of the standard depth.
Alternatively, we can co-add multiple frames (or, much easier, the
atlas images) taken of a given region of sky
scanned at sidereal rate; this requires that the code to co-add atlas
images must be developed.
- (b)
- Bright galaxies with well measured target selection parameters are artificially redshifted and inserted at random locations into the imaging data. We then see what fraction of them are recovered as targets after running through the data reduction and target selection pipelines. This test will be a lot of work.
- 4.
- Using repeated photometric scans of the same regions under varying observing conditions.
- 5.
- By applying the target selection algorithm to scans over a wide range of positions on the sky.
- 6.
- Same as [2].
- 7.
- The 10 square degree survey mentioned in [3(a)] would yield
only 100 BRG's, which may be inadequate to explore the BRG target
selection.
There are 3 areas to test:
- (a)
- The surface density limits and scatter propagation may be tested by observing fields without any color cut and with a relaxed luminosity cut.
- (b)
- Photometric measurements (including known problems with Petrosian magnitudes e.g, for cD galaxies) may be tested with a 1/4 sidereal scan of 10 square degrees providing higher signal to noise.
- (c)
- The measurements of luminosity and rest frame color may be tested with spectra and spectrophotometry of a large number of targets.
- 8.
- Same as [4].
- 10.
- By spectroscopic follow-up of quasar targets in fields covering a range of sky positions (since the efficiency may vary strongly with stellar density). We need to quantify how many fields are needed.
- 11.
- Scan areas where there have been extensive previous quasar surveys to i' = 19, preferably using multiple methods.
- 12.
- Same as [2] and [6].
- 13.
- The fraction of targets untiled should be a tunable parameter in the tiling algorithm itself. We just have to ensure that this requirement is met as the survey proceeds.
- 14.
- The fuzziness of target selection cuts are a series of tunable parameters, which will be set with the worst-case allowable photometric errors in mind.
6.5 Estimated timescale for confirming these requirements
Commissioning of target selection is the single largest task of the scientific commissioning period; successful completion of these tasks will largely define the end of the commissioning period and the beginning of the survey proper. Several of the tests require observations that are at least 1% and preferably several percent of the full survey observations, although we will push to make this shorter if at all possible. Plans for the imaging and spectroscopy needed for quasar target selection describe what is needed for quasars.
6.6 Resources needed for carrying out these tasks
These tests will require reduction of large amounts of imaging and spectroscopic data, using the production system at Fermilab, and several person-years of analysis and examination of the results.
6.7 Quality Assurance
During the commissioning period, we will be able to measure the
standard deviation of the number of galaxy, BRG, and quasar
targets of different types as a function of area, e.g., in
![]() ,
, ![]() , and
, and
![]() patches.
The situation will be trickier for quasar targets than for galaxies/BRGs
because the surface density will change systematically with sky
position (because of the varying number of false positives (stars)
with position), so we will need to develop a model for the mean and
standard deviation of target numbers as a function of position.
patches.
The situation will be trickier for quasar targets than for galaxies/BRGs
because the surface density will change systematically with sky
position (because of the varying number of false positives (stars)
with position), so we will need to develop a model for the mean and
standard deviation of target numbers as a function of position.
We will also be able to measure the distribution function of the fractions of galaxy/BRG, and quasar targets that are spectroscopically confirmed as the expected kind of object and yield measured redshifts, and we will be able to measure the rms difference between photometric and spectroscopic redshifts of BRGs.
Quality assurance tests for target selection that should be continued throughout the survey are:
- 1.
- After target selection but before spectroscopy:
- (a)
- Investigate cases in which the number of targets in a given class
is more than
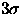 away from the expected number on any of these
area scales.
away from the expected number on any of these
area scales.
- (b)
- Monitor the fraction of targets that are successfully assigned a fiber (not lost because of minimum spacing or some other conflict or error). It is not clear what our advance expectations should be here, so we will have to build up experience over time and search for any large deviations.
- (c)
- Examine the number of targets selected per frame as a function of seeing, sky brightness, reddening, airmass, and so on.
- 2.
- After spectroscopy:
- (a)
- Investigate cases where the fraction of targets that are confirmed as members of the expected class and yield successful redshifts falls outside of the expected range.
- (b)
- Compute the rms error of photometric redshifts. Investigate cases where this error is substantially different from the expected error.
- 3.
- As the survey proceeds:
- (a)
- Investigate correlations between the number of selected targets and the imaging observing conditions (seeing, moon, etc.) or sky position.
- (b)
- Investigate correlations between the fraction of successful redshifts and spectroscopic observing conditions.
6.8 Who's in charge
The galaxy and quasar working groups (and in particular, their respective chairs, Michael Strauss and Don Schneider) are in charge of seeing that their science targets are properly selected.3.7 Enhanced Goals
The quasar efficiency will be 80% for i'<19 quasars in the cap, and 60% for i<18 in the skirt.5.2.6 Further Test Year Tasks
- 1.
- The photometric redshift relation must be determined. This requires SDSS photometry in regions of sky with large numbers of faint galaxies with redshifts in the literature.
- 2.
- The TBDs on efficiency for quasar target selection must be finalized; this will then allow us to turn the numbers of quasar targets into a photometric limit. More could be written on the quasar science goals, to make clearer how to design the quasar target selection algorithm.
- 3.
- The Petrosian parameters, and other parameters associated with galaxy target selection (cf., the galaxy target selection document) must be fine-tuned, and confirmed to be robust to blending, sky level, and so on.
- 4.
- We must determine a reasonable surface brightness limit for the main galaxy sample. We plan a surface brightness cut, in order to get reasonable signal-to-noise ratio spectra in our 45-minute exposures. However, low surface brightness galaxies often have strong emission lines, making it easier to measure redshifts.
- 5.
- Sanity checks should be carried out of the galaxies selected as
Bright Red Galaxies:
- (a)
- Do they tend to be BCGs? That is, do they tend to lie in the centers of rich clusters?
- (b)
- Can we actually obtain redshifts of these objects at the photometric limit?
- 6.
- The ROSAT target selection algorithm must be finalized. It is not even described in the document above.
- 7.
- It has been suggested that we obtain multiple spectroscopic observations of a given field, and determine the fraction of galaxies, BRGs, and quasars that have a redshift successfully measured one time and not the other.
6.11 What's Missing; What needs to be done
- 1.
- Requirements on the ROSAT target selection algorithm.
- 2.
- Incorporation of quasar and galaxy test year plans.
- 3.
- Further refinement of the quasar target selection goals.
- 4.
- Discussion of requirements on FIRST.
- 5.
- Clarification of responsibilities throughout.
- 6.
- Discussion of requirements on targets other than galaxies and quasars.
7 Spectroscopic Requirements
This section has substantial input from Don Schneider.See § A.5 for a brief summary of the spectrograph design parameters. These requirements are drawn largely from this document on spectrograph specifications; See that document for more details.
7.1 Spectroscopic Throughput
7.1.1 Quantitative Requirements
- 1.
- The overall throughput of the spectrographs at all wavelengths should be 90% or higher than that given in Figure 11.8 of the Black Book, for more than 95% of the fibers. This includes the throughput of all components: fibers, the spectrograph optics, and the CCDs.
- 2.
- The average throughput of the fibers in each 20-fiber harness should exceed 90%, with a minimum in any fiber of 87% (not including broken fibers). This requirement can be found here.
- 3.
- The rms fiber-to-fiber throughput variation at a given wavelength shall not exceed 4%.
7.1.2 Scientific Justification
The primary goal of the spectroscopic observations is to determine the redshift of the observed objects; this demands relatively high signal-to-noise ratio spectra over a wide wavelength range. The absolute throughput requirements are needed to produced the required signal-to-noise ratio for the most challenging objects (galaxies with brightnesses at the spectroscopic limit). If the fiber-to-fiber variations are too large, the spectra of a considerable fraction of the targets will be of insufficient quality to determine a redshift.7.1.3 Consequences of Not Meeting Requirements
The throughput of the spectrograph has a direct relation to the amount of integration time required to obtain a spectrum of sufficient signal-to-noise ratio. A lower throughput translates into longer spectroscopic exposures, thus either lengthening the survey or reducing the fraction of the survey that can be observed spectroscopically.7.1.4 How do we determine if these requirements are met?
The fiber throughputs can be measured in the lab; the fibers have been demonstrated to meet specifications cleanly (see here for details). The total system throughput can be measured from every exposure (in photometric conditions) from the spectrophotometric standard(s).
7.1.5 Quality Assurance
The fiber-to-fiber variations can be monitored in every exposure for all wavelengths using the flat field. Throughput curves (relative if not necessarily absolute) can be obtained on every exposure from the spectra of the spectrophotometric standards. It should also be possible to make crude throughput calculations for every object using the SDSS imaging data.7.1.6 Who's in charge
The Spectroscopic Scientist.7.2 Spectroscopic Wavelength Coverage, Resolution and Stability
7.2.1 Quantitative Requirements
- 1.
- The spectrographs should have continuous coverage from 3900-9100Å.
- 2.
- The rms deviation of measured wavelength scale from the arc lines shall be less than 0.1Å (blue spectrograph) and 0.2 Å (red spectrograph) for all fibers over the full spectral range.
- 3.
- FWHMs of unblended arc lines, in pixels, in a given fiber will have an rms dispersion of less than 5% of the mean FWHM.
- 4.
- FWHMs of unblended arc lines, in pixels, at a given wavelength will have an rms dispersion of less than 5% of the mean FWHM at that wavelength.
- 5.
- The FWHM of unblended sky lines in all the spectra will be less than 1.05 times that of arc lines in the same part of the detector.
- 6.
- The minimum spectral resolution (
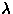 /FWHM) in a 15-minute
exposure at any wavelength in any fiber is 1800.
These last two items are requirements on instrument flexure (the Black
Book quotes flexure of
/FWHM) in a 15-minute
exposure at any wavelength in any fiber is 1800.
These last two items are requirements on instrument flexure (the Black
Book quotes flexure of 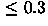 pixel for exposures from the zenith to
airmass of 1.7), on the grating, and on the optics (telescope +
spectroscopic corrector + collimator).
pixel for exposures from the zenith to
airmass of 1.7), on the grating, and on the optics (telescope +
spectroscopic corrector + collimator).
- 7.
- Flat-fielding must be done so as to be insensitive to any flexure of the spectrographs.
- 8.
- The cross-talk between adjacent fibers (i.e., the fraction of the light from a given fiber that falls within the aperture of the adjacent fiber) will be less than 1%. It remains to be seen what the spectrographs will actually deliver.
7.2.2 Scientific Justification
- 1.
- The large spectral range is required to obtain accurate redshifts of the targets. Galaxy absorption lines used for redshifts lie primarily in the 3900-6000 Å range, which will be found on the blue chip for low redshift, moving to the red chip for galaxies at redshifts of several tenths. Moreover, high redshift quasars might be detected only in the 6000-9100Å range.
- 2.
- The accuracy of the wavelength scale is needed to produce galaxy
redshifts of sufficient quality to investigate the distribution and
motions of galaxies on scales of
 Mpc or smaller.
Mpc or smaller.
- 3-5.
- The stability requirements place flexure limits on the spectrograph, preserving the integrity of the wavelength scale. The optical design of the spectrograph (see Table 11.2 of the Black Book, page 11.14) delivers 4% variations in FWHM diameters of unresolved lines, after convolution with the 3-pixel aperture of the fibers. Perhaps we also need a requirement on encircled energy.
- 6.
- The minimum resolution matches the typical width of a galaxy absorption line.
- 7.
- If there is appreciable flexure, the object exposures and flat-fields taken through the fibers will not line up, giving biased results. Thus this can be read either as a requirement on the flexure (also an issue for the previous item), or if flexure turns out to be large, a requirement that uniformly illuminated flats be taken.
- 8.
- Cross-talk between fibers gives contaminated spectra, yielding unreliable redshifts.
7.2.3 Consequences of not meeting requirements
The accuracy of the wavelength scale translates directly into the accuracy of the redshift measurements. For any reasonable expected error, this will be negligible for quasar redshifts, but will significantly impact both galaxy and quasar absorption line redshifts. Flexure in the wavelength direction produces a degradation in the wavelength scale and resolution; flexure in the perpendicular direction reduces the signal-to-noise ratio of the spectrum and hence the accuracy of the redshift. Crosstalk degrades the signal-to-noise ratio of the spectra, and is likely to give biased redshifts.
Failing to meet the resolution requirement will result in a
significant reduction of the ability to detect and measure absorption
and emission features (especially when the absorption lines become
crowded, as in the Lyman ![]() forest), and to measure the redshift
and velocity dispersion of galaxies and the redshifts of quasar
absorption lines.
forest), and to measure the redshift
and velocity dispersion of galaxies and the redshifts of quasar
absorption lines.
7.2.4 How Do We Determine if These Requirements are Met?
All of these requirements can be determined from the accuracy of the wavelength solutions from arc lines, and the width of arc and sky lines measured. Arcs taken before and after each exposure give a measure of the effects of flexure.The cross-talk can be determined by examining the extracted spectrum of sky fibers adjacent in the slit to bright stars.
7.2.5 Quality Assurance
A monitoring program using the information described in § 7.2.4 must be put in place. The properties of the arc/sky lines that are produced in every series of observations must be recorded and checked on a periodic basis.
7.2.6 Who is in Charge?
The Spectroscopic Scientist.7.3 Spectroscopic Reliability
This section is waiting for further input from Steve Kent.7.3.1 Quantitative Requirements
- 1.
- The coaddition of three 900 sec exposures in photometric conditions of an elliptical galaxy at redshifts between 0.0 and 0.3 whose r' fiber magnitude is less than or equal to 19.5 will yield a redshift with an rms statistical error of 30 km/s.
- 2.
- We need a separate requirement here on systematic errors in redshifts. This is much more difficult to design a test for.
- 3.
- Correctly classify 95% (enhanced goal of 98%) of the
quasars (for the present purposes, defined as objects with at least one
emission line with an equivalent width> 10Å) with
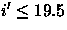 .
Of the quasars not identified as
such, 99% will be classified as ``unknown class" (i.e., not identified
as a galaxy, star, etc).
.
Of the quasars not identified as
such, 99% will be classified as ``unknown class" (i.e., not identified
as a galaxy, star, etc).
- 4.
- A maximum of 1% of the Galactic stars will be assigned redshifts larger
than 0.01 and have redshifts that differ by more than
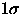 from 0.0.
A maximum of 1% of the galaxies with r' < 18.2 (Petrosian)
without strong broad emission lines will be classified as quasars.
This requirement needs work, as it is rather difficult to measure
failure rates that are this small.
from 0.0.
A maximum of 1% of the galaxies with r' < 18.2 (Petrosian)
without strong broad emission lines will be classified as quasars.
This requirement needs work, as it is rather difficult to measure
failure rates that are this small.
- 5.
- The redshifts of BAL QSOs will be determined to an rms accuracy of 0.02 and the redshifts of non-BAL QSOs to an rms accuracy of 0.005.
7.3.2 Scientific Justification
Investigations of small scale/cluster structure with galaxies near the photometric limit require the stated galaxy redshift accuracy. To efficiently analyze the data one needs to be certain that the reliability of the classifications and the redshifts is high.
7.3.3 Consequences of not meeting requirements
Failure to reach the redshift accuracies for the galaxies will severely limit the investigation of small scale/cluster structure. The quasar redshift accuracy limit is driven more by what should be possible than by scientific goals; the primary goals of the survey can be met with errors several times larger than the stated limit. Larger quasar redshift errors would adversely impact areas such as quasar absorption lines and gravitational lenses.
Unless the classification reliability meets the requirements, it will not be possible to trust the automated classifications and each spectrum will have to be examined, and perhaps analyzed, by hand.
7.3.4 How do we determine if these requirements are met?
Simulated spectra will provide an important test of the redshift software, but this will not be entirely satisfactory; all we can say is that if the software cannot meet the requirements on simulated spectra we can be assured that we won't be able to determine redshifts in the real data.Observational tests of the reliability can be done by observing the same (or more than one) field several times and examining the distribution of measured redshifts for each of the objects.
In addition, we could do multiple short exposures of a given field, and ask how many need to be co-added before the redshift reliability meets specifications. This needs to be fleshed out.
7.3.5 Quality Assurance
Some small fraction of the objects in the overlapping areas should be observed twice. Some fraction of the spectra and results will be inspected by hand on a continuing basis to monitor the performance of the software.7.3.6 Further Tasks
Some of these items overlap with operations tasks, below.- 1.
- We need to determine the minimum number of sky fibers necessary for adequate sky subtraction.
- 2.
- We need to determine the number of fibers needed for calibrations (spectrophotometry, reddening, and telluric absorption correction).
- 3.
- We need to finalize the final set of calibration exposures needed with each set of spectroscopic observations (dithered and undithered flat fields, arc, and four-pointing observations for spectroscopy).
- 4.
- We need to finalize the spectroscopic templates (via PCA, standard stars, or otherwise) to be used in the cross-correlation.
7.3.7 Who is in Charge?
The Spectroscopic Commissioner.7.4 Spectrophotometric Accuracy
This section is abstracted from a document by Bob Nichol. It has been worded as a requirement on spectroscopic operations. It is understood that formal requirements on spectrophotometric accuracy on each spectrum are probably unreachable.7.4.1 Quantitative Requirements
The spectroscopy should be carried out in such a way to allow spectrophotometric calibrations to be done. This implies that:- At least three bright (
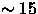 th magnitude) calibration stars must be
spectroscopically observed per SDSS spectroscopic plate. The star
should possess a smooth spectral energy distribution i.e. F
subdwarf star.
th magnitude) calibration stars must be
spectroscopically observed per SDSS spectroscopic plate. The star
should possess a smooth spectral energy distribution i.e. F
subdwarf star.
- The position of each fiber relative to the center of its target must be determined with an accuracy of < 0.5'' for greater than 85% of the fibers.
7.4.2 Scientific Justification
The above operational requirements are put in with the scientific aim of yielding an rms error in the relative spectrophotometric calibration averaged in 200Å chunks over the entire spectrum no more than 10%.
The main science driver for SDSS spectrophotometry is the detailed study of the stellar content of galaxies and its evolution with environment and redshift. We also would like to have one of the main scientific products of the SDSS, the spectra of over one million objects, be fully calibrated.
Spectrophotometry for SDSS galaxies would also help in the redshift determinations of galaxies as it would allow direct fitting, in wavelength space, of the galaxy data with well-known spectrophotometric templates.
The requirement on the brightness of the calibration stars is to ensure that the PT can obtain a high signal-to-noise detection of the star, through the intermediate-band spectrophotometric filters, in a short integration time. The star cannot be too bright, to minimize the cross-talk between fibers. Three stars are needed in case some turn out to be variable, and may be useful in non-photometric conditions if the atmospheric transparency varies appreciably across the field of the telescope. Finally, note that one can only do a poor job of synthesizing the spectrophotometry from the combination of the SDSS broad-band photometry, as one has only three points (g', r', and i') included in the spectral coverage.
7.4.3 Consequences of Not Meeting Requirements
- 1.
- From studies of synthesized galaxy spectral energy distributions
(Bruzual & Charlot 1996), the rms error in the relative
spectrophotometric accuracy must be less than
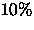 to conclusively
differentiate between galaxies of different ages and
metallicities.
to conclusively
differentiate between galaxies of different ages and
metallicities.
- 2.
- Spectrophotometric accuracy will greatly degrade as the fiber position relative to the galaxy becomes more uncertain.
- 3.
- If any plate does not have calibration stars, neither absolute nor relative spectrophotometry can be done for any of the galaxies on the plate, except crudely via their broad-band photometry.
- 4.
- If spectrophotometry is used in the redshift determination, and if spectrophotometry can't be done for all exposures, then we run the risk of non-uniform completeness in the redshift determinations.
7.4.4 How do we determine if these requirements are met?
The relative spectrophotometric accuracy can be determined with observations of known F subdwarfs with well-determined spectrophotometry through a series of SDSS spectroscopic fibers in turn.
7.4.5 Test Year Tasks
- 1.
- Observe a star with published spectrophotometry with the SDSS spectrographs. Observe the same star with the SDSS camera and the PT using the spectrophotometric filters. Repeat the experiment in photometric and non-photometric conditions, and quantify the reproducibility of the spectrophotometric results, and the added improvement that the diamond-pattern raster scan gives.
- 2.
- Determine the correct exposure time for the diamond-pattern raster scan; it is now nominally 1 minute per pointing.
- 3.
- Test the target selection criteria of F subdwarfs from the main SDSS photometric data. Determine the magnitude range over which they should be selected.
- 4.
- Determine the required number of spectrophotometric calibration stars per spectroscopic plate, given variations of atmospheric transparency across the plate.
- 5.
- Obtain roughly 10 photometric nights of observations of spectrophotometric standards with the Photometric Telescope, using the 10 intermediate-band spectrophotometric filters. This is required to calibrate the network of spectrophotometric calibration stars. Note that this need not be done before the start of operations.
- 6.
- Carry out checks of the accuracy of the red-blue merging of the spectra in the spectroscopic pipeline, and the fiber-to-fiber throughput corrections.
7.4.6 Who's in charge
The Spectroscopic Scientist is in charge of overseeing the spectrophotometric commissioning discussed here, and, in collaboration with the Project Scientist, determine whether the tests have been successful or not.
8 Operations and Strategy
This section was written by Rich Kron.See the document here for an earlier draft of the present.
8.1 Duration of Survey
8.1.1 Quantitative Requirements
The survey shall be completeable within 5 years. This requirement assumes that the data meet quality standards described elsewhere. The spirit of the requirement relates to factors that are within our control; if the atmospheric conditions are less favorable than we have assumed, the survey will take longer, of course.
8.1.2 Scientific Justification
The survey has been designed around the goal of completion within five years. The cost of the survey depends on its duration.
8.1.3 Consequences of not Meeting Requirement
Skilled people move onto other projects. We lose credibility with funding agencies. We will run out of money.
8.1.4 How do we Determine if this Requirement is Being Met?
The progress of the survey is reckoned by the area of sky scanned and accepted into the science database, and the number of spectra obtained (or tiles exposed) and accepted into the science database. This rate is compared to the necessary rate, which is derived from the strategy planning tool.
8.1.5 Estimated Timescale for Confirming this Requirement
Tuning the efficiency of operations will take some time - at least a year into the survey. Thus, while we will have rate data immediately, the asymptotic rate of covering the sky will not be certain for at least a year, and more realistically well into the second observing season. An additional complication is the fact that the rate of taking data at the end of the survey may be quite a bit slower, as we struggle to fill up holes in the sky coverage.
8.1.6 Resources Needed
There will be instances where a trade-off between survey speed and available SDSS resources will be required (for example, it costs more to repair things faster). The overarching idea is that Operations should have the planning tools needed to maximize the amount of ``survey quality" data, given the available resources of time, money, and people.
An important resource is the strategy planning tool; it needs to be exercised further to optimize long-term efficiency of the survey.
8.1.7 Who is in Charge?
Director of Program Operations.
8.2 Safety
8.2.1 Quantitative Requirements
All relevant systems must be critically reviewed to evaluate the potential for hazards to humans and equipment. A comprehensive review will be undertaken of each subsystem before routine operations begin, and subsequent reviews will be undertaken as necessary. Any safety issues must be resolved quickly and completely.
8.2.2 How do we Determine if this Requirement is Met?
A program of routine safety audits will be established. Reviews and results of actions taken will be documented. A reporting system will be established for logging incidents and the response taken.
8.2.3 Resources Needed
We need to establish an operations system - and culture - that anticipates hazards before incidents happen. An infrastructure needs to be created for planning, tracking, and evaluating the safety audits, and properly reacting to the reports.
8.2.4 Who is in Charge?
Program Director.
8.3 Spectroscopic Plug Plate Delivery Rate
8.3.1 Quantitative Requirements
After the first year of spectroscopic observations, the rate of progress of the survey shall never be limited by the availability of plug plates or cartridges.
8.3.2 Scientific Justification
Once a supply of plates has been built up, the spectroscopic observations are within our control. The requirement simply states that the usage of the telescope will not be limited by something within our control. The mean rate of plate consumption is 50 per month. This requirement states that at all times, there be an adequate inventory of pluggable plates at APO at all reachable LST's that spectroscopy is not limited by the availability of plates. Of course, as we near the end of the survey, we will run out of sky to be observed.
8.3.3 Consequences of not Meeting Requirement
Observing time is lost or used less effectively than otherwise possible.
8.3.4 Resources Needed
The timely fabrication of new plates is a major part of what SDSS Operations has to do. The specifics are covered in subsequent requirements.
8.3.5 Who is in Charge?
Program Director.
8.4 Photometric Reduction
8.4.1 Quantitative Requirements
The achievable elapsed time between obtaining photometric data (tapes out) and being able to observe that part of the sky spectroscopically (plates in) is required to be normally a full year, with 26 days on an occasional basis (i.e., of order three times per year). For two eight-hour scans, this fast track should be as follows:
| fast track | ||
| ship tapes to FNAL | 1 | |
| pipelines through target selection | 15 | |
| plate design | 1 | |
| plate fabrication | 8 | |
| ship plates to APO | 1 | |
| total | 26 |
These figures are based on the following considerations:
- 1.
- Tapes written after each night of observation are shipped to Fermilab such that they arrive the following day, regardless of the day of the week.
- 2.
- The mean rate of acquiring new imaging data each month is about 24 hours per month, spread over typically 4 nights. The data from a given dark run can be processed within 15 days of the end of that dark run. Notice that this includes running all relevant pipelines, and stuffing the operational database.
- 3.
- Given a decision to tile a certain region of sky, it shall be possible to generate hole positions for up to 50 plates within 1 day of that decision.
8.4.2 Scientific Justification
This requirement is very much in support of the previous requirement that adequate spectroscopic plates be available on the mountain at all times.
Reducing the data at least as fast as the data are obtained prevents the processing from limiting the speed of the survey. Fast processing allows errors to be recognized early, thus preventing observing time from being wasted. The specific times are designed to enable spectroscopic observations two dark runs after the imaging data are obtained.
Timely and convenient access to the data by the collaboration is stipulated in the Principles of Operation, and is another major part of SDSS Operations.
8.4.3 Consequences of not Meeting Requirement
The roughly one-month turn-around is intended to avoid losses in efficiency from regions of the sky setting in the West, and also to respond to strategically important opportunities (filling in gaps, acquiring data at extreme declinations, etc.).
8.4.4 Resources Needed
The Science Database needs to be created and commissioned.
8.4.5 Who is in Charge?
Program Director.
8.5 Overhead on Observations
8.5.1 Quantitative Requirements
Intervals of dark time can be classified as: time exposing on the sky; time lost due to atmospheric conditions; and everything else. The ``everything else" shall be no greater than 320 hours per year (i.e., roughly the time per year needed for taking photometric data). This contingency is intended to cover inefficiencies like: instrument exchange time; calibrations during dark time; time elapsed between the determination of clear weather and the initiation of taking data; photometric ramp time; inefficiency at the end of a night; and scheduled and unscheduled down-time due to hardware and on-line software problems, repairs, and maintenance.
In more detail, the total overhead associated with spectroscopic exposures, i.e., the time not used for on-the-sky integration, shall be less than 22 minutes per exposure. The time required to switch between imaging and spectroscopy (counting from the end of sky integration to the beginning of sky integration) shall be less than 30 minutes.
8.5.2 Scientific Justification
This requirement is intended to ensure that the maximum amount of astronomically usable observing time is actually available, in order to minimize the time-to-completion for the survey.
8.5.3 Consequences of not Meeting Requirement
This is really a finer-grained version of the requirement in § 8.1 (and is in fact derived from it), focusing on things that are within our control.
8.5.4 How do we Determine if this Requirement is Met?
The night logs should enable the accounting for time to be easily reconstructed.
8.5.5 Resources Needed
If we suffer extended periods of unscheduled down-time, then substantial resources may be required to meet this requirement. If the instrument exchange times are unacceptably long, then substantial re-working may be necessary.
8.5.6 Who is in Charge?
Program Director.
8.6 Spectroscopic Reduction
8.6.1 Quantitative Requirements
The elapsed time between acquisition of spectroscopic data and the availability to the SDSS collaboration of reduced spectra (fluxes, redshifts, classifications) shall be 15 days, with a goal of 10 days. Perhaps an elaboration is needed for the case in which both photometric and spectroscopic data are competing for reduction resources at Fermilab.
8.6.2 Scientific Justification
Timely and convenient access to the data by the collaboration is stipulated in the Principles of Operation, and is another major part of SDSS Operations. This particular requirement enables QA by distributed scientists on a timescale shorter than a lunation.
8.6.3 How do we Determine if this Requirement is Met?
The time taken from data acquisition to placing the reduced version into the Science Database is easy to determine. Less easy to determine is whether the design of the database is adequately responsive to the scientific goals of the various SDSS institutions. Perhaps we need a separate requirement on this.
8.6.4 Resources Needed
The Science Database needs to be created and commissioned.
8.6.5 Who is in Charge?
Program Director.
8.7 Requirements on the Photometric Telescope
Note the overlap of this section with § 4.8.7.1 Quantitative Requirements
The Photometric Telescope is required to measure extinction coefficients for each hour during photometric scanning; specifically, it shall be capable of calibrating intervals as short as 1.5 hours of 2.5-m scanning data. It is also required to obtain accurate photometry of stars that are faint enough to be unsaturated in the 2.5-m telescope scans, spaced approximately every 15 degrees along each scan. The timing of the observations of these patches must not limit the schedule for data processing; in particular, the secondary patches have to keep up with (or even be ahead of) the 2.5m imaging.
8.7.2 Scientific Justification
The density of calibrations, in angle in the sky and in time, is intended to be sufficiently great that the photometric precision is not limited by that factor. The timing requirement comes from the principle that the survey should be fundamentally limited by 2.5-m telescope operations, as opposed to the throughput of any of the other SDSS systems (otherwise, the rate of progress of the survey would be potentially limited by too many other bottlenecks).
8.7.3 Who is in Charge?
Program Director.
8.8 Requirements on Survey Strategy Tools
8.8.1 Quantitative Requirements
- 1.
- A planning tool used at Fermilab must be implemented that helps determine when a tiling solution should be undertaken, and what the specific parameters should be (boundaries of the region, etc.). Having produced a tiling solution, a tool must exist for prioritizing the plates in the sense of orders placed for drilling, and their shipment to APO.
- 2.
- A planning tool used by the Observers must be implemented that picks the best scans to do on a particular night (in particular, the upcoming night), or the best sequence of spectroscopic plates. The tool must be capable of making real-time adjustments to the plan, for example if clouds suddenly part in the middle of a night.
8.8.2 Scientific Justification
These tools help minimize the time-to-completion for the survey by enabling strategic options to be explored.
8.8.3 Resources Needed
Code needs to be developed that, among other things, is tied into the Operational Database (because the assessed quality of existing data needs to be known) and has good visualization tools.
8.8.4 Who is in Charge?
Program Director.
8.9 Adjustment of Spectroscopic Exposure Time
8.9.1 Quantitative Requirements
Spectroscopic exposures obtained in unfavorable conditions (cirrus, poor seeing, reddening) need to be lengthened a priori, to yield signal-to-noise ratios close to those one would get for the same objects under ideal conditions without reddening. A system must be implemented to monitor the integration; to estimate the necessary extra time required; and to adjust the exposure time accordingly.
8.9.2 Scientific Justification
The intent is to obtain uniform signal-to-noise ratio in the spectra for a particular monochromatic flux.
8.9.3 Resources Needed
Code needs to be developed to take the known airmass and measured throughput of the atmosphere from the guide fibers, and feed the information automatically to the program actually running the spectrographs.8.9.4 Quality Assurance
The signal-to-noise ratio of the spectra will be tabulated as a function of apparent magnitude.8.9.5 Who is in Charge?
Program Director.
8.10 Maintenance of Optical Throughput of Components
8.10.1 Quantitative Requirements
- 1.
- Operations shall monitor the throughput of the separate components along the optical train of both the 2.5-m telescope and the Photometric Telescope on a timescale that is short compared to detectable changes. Operations shall mitigate any effects that could lower the as-delivered instrumental throughput (or other performance).
- 2.
- A practical system must be implemented for cleaning optical surfaces on a periodic basis as needed.
- 3.
- A practical system must be implemented to handle mirrors for periodic recoating. The allowable interval that either telescope is down for this purpose is 15 days per year.
8.10.2 Scientific Justification
This is required to keep the uniformity of the data high, and in particular, to maintain high throughput of the optical system.
8.10.3 Resources Needed
A variety of special-purpose hardware and handling fixtures is needed for monitoring optical surfaces. A detailed plan for the monitoring and cleaning must be developed.
8.10.4 Who is in Charge?
Program Director.
8.11 Requirements on Spectroscopic Fibers and their Handling
8.11.1 Quantitative Requirements
- 1.
- There is *NO* requirement to design a plate to be used with a particular cartridge (i.e., taking into account its particular suite of broken fibers).
- 2.
- A harness should be replaced when more than 5% of its fibers become unusable (e.g., by becoming broken), based on the scientific need to keep the spectroscopic sampling as complete as practically possible. That is, a harness should be replaced when missing fibers are comparable in number to the number of objects missed in target selection because of the 55'' rule.
- 3.
- Operations must implement a suitable procedure for replacing harnesses.
- 4.
- The plug plates need to have indicators to guide the pluggers according to groupings of 20 fibers (but there is no further requirement concerning which fiber goes into which hole). Other special holes for special fibers (e.g., guide star fibers) must also be indicated on the plate.
- 5.
- The association of fiber number with the hole in which the fiber was plugged must be accomplished automatically, with no more than one pair of misidentified fibers per 10 plates.
- 6.
- No more than one fiber per plate can drop out due to handling, from the time it is put in the fiber mapper, to the time it is observed on the telescope.
8.11.2 Scientific Justification
These requirements allow efficient spectroscopic observations, and accurate association of the spectroscopic and photometric data.8.11.3 Who is in Charge?
Program Director.
8.12 Miscellaneous
- 1.
- It shall be possible to change the target-selection parameters twice per year for Serendipity objects as determined by the Serendipity Working Group.
- 2.
- It shall be possible for the Serendipity Working Group to give hand-picked lists of objects to target selection.
- 3.
- One copy of all of the data tapes sent to Fermilab as shall be archived at (or nearby) APO for two years or more. Up until the end of APO observations, the amount of data lost per year due to the corruption of archived data shall be economically equivalent to less than 0.5 night per year of repeated observations.
- 4.
- Sufficient spectroscopic analysis must be accomplished on the mountain to determine whether a plate exposed during the previous night can be unplugged so that the cartridge can be used for another plate. The requirement is that at least 80% of the working hours for the plugging staff be within the interval 9 AM - 5 PM local time.
- 5.
- Sufficient quality-assurance checks must be undertaken at the mountain so that no more than 20% of all of the data sent to Fermilab as ``good'' are rejected on the grounds of not satisfying the TBD science quality and uniformity criteria.
8.13 What's Missing
There are a number of requirements which are not discussed in this section:
- 1.
- A requirement on the maximum allowable size of any contiguous regions not covered by the imaging at the end of the survey (see the discussion in § 3).
- 2.
- Requirements on sky brightness, transparency, and seeing beyond which imaging would not be done. These could be different for North and South observing. Criteria for determining these limits could include: These will tie into requirements on photometric depth and uniformity, and on accuracy of target selection; see those sections for more detail. A strawman suggestion for the seeing requirement is no worse than 1.2'' over the photometric array (not counting the u' chips, which will be strongly affected by differential chromatic aberration at large airmass).
- 3.
- Requirements on sky brightness, transparency, and seeing beyond which spectroscopy would not be done; see § 7. The principal criterion for determining these limits will be signal-to-noise ratio of the spectra; see also § 6.
- 4.
- A check that the signal-to-noise ratio improves as expected as the Southern stripe data are co-added. If it doesn't for some reason, our strategy for Southern Stripe observing will change. We will want to know this sooner rather than later.
- 5.
- Further requirements on regular maintenance of instruments, with adequate spares on the mountain, etc. See § 8.5.
- 6.
- A requirement that we be able to acquire spectroscopic fields quickly even if the telescope does not meet pointing specifications. Alan Uomoto has suggested using a 10'' Celestron + CCD strapped to the telescope for this purpose; see here. This would keep downtime to a minimum.
- 7.
- A requirement on the acquisition of uniformly illuminated flat fields for spectroscopy, and for the astrometric chips.
- 8.
- A requirement on the maintenance of adequate focus on the spectroscopic exposures. This is part of the throughput requirement on spectroscopy.
- 9.
- Perhaps most importantly, we don't have specific requirements on QA. This is incorporated into this document throughout, of course, but we could focus on it more directly in this section.
Appendix: Basic parameters of the survey
This section has been written by Steve Kent. This section tabulates useful parameters, but is not a set of requirements per se.- 1.
- The Northern Survey boundary is defined by an ellipse as drawn
on a polar equal-area projection of the sky centered on the North Galactic Pole.
The ellipse is centered on
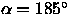 ,
,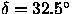 (J2000), with axes
(J2000), with axes 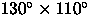 . The major
axis is rotated clockwise by 20
. The major
axis is rotated clockwise by 20 relative to an east-west orientation
(and thus, is tilted to higher declination at greater right ascension).
relative to an east-west orientation
(and thus, is tilted to higher declination at greater right ascension).
Basis: The ellipse is aligned to avoid interstellar reddening as much as possible, and to maximize the length of photometric scans. The ellipse center in declination is chosen to center one stripe on the Celestial Equator. - 2.
- There are three stripes that will be done in the Southern
Galactic Cap. They are roughly given by:
- (a)
- Stripe 76:
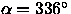 to
to 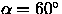 ,
, 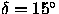 at
at 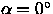 .
. - (b)
- Stripe 82:
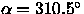 to
to 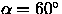 ,
, 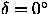 at
at 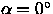 .
. - (c)
- Stripe 86:
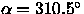 to
to 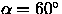 ,
, 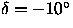 at
at 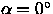 .
.
- 3.
- Nominal PSF FWHM of the imaging survey: 1 arcsec
Basis: PSF should be limited by typical APO site seeing (0.8 arcsec), combined with intrinsic PSF of the telescope optics. See § 3 for more. - 4.
- The imaging limiting magnitude: u'=22.3, g'= 23.3, r'=23.1, i'=22.3, z'=20.8
(5
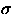 limit for point sources).
limit for point sources).
Basis:- (a)
- This is the expected limiting magnitude for the camera and telescope built with good engineering practice.
- (b)
- The selection of quasars for spectroscopy will involve u' and z' photometry close to their respective photometric limits.
- 5.
- Roughly 150,000 QSO candidates will be targeted spectroscopically
Basis: The PoO defines the limiting magnitude for QSO spectroscopy to be r' = 19, which yields an estimated 100,000 QSOs. With an estimated 65% success rate for QSO targeting, this yields the value above. For more detail on this and the following item, see § 6. - 6.
- The limiting magnitude for galaxy spectroscopy is
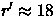 (where the current plan is to use Petrosian magnitudes).
(where the current plan is to use Petrosian magnitudes).
- 7.
- The imaging is done in a series of scans at the sidereal rate
drawing great circles
in the sky. The spacing between successive stripes should be
2.5
 in
in 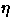 .
.
A.1 Basic parameters of the telescope
See here for details.- 1.
- Nominal optical design:
- (a)
- Primary mirror diameter: 2500 mm
- (b)
- Primary mirror focal ratio: 2.25
- (c)
- Secondary mirror diameter: 1140 mm
- (d)
- Nominal focal plane pixel scale (spectroscopic mode): 16.53 arcsec/mm
- (e)
- Primary mirror maximum z position range: 13 mm; see ( here)
- (f)
- Maximum range of scale adjustment: 0.7% (same reference)
- (g)
- Focal plane radius (spectroscopic mode): 327 mm
- 2.
- Mechanical parameters (weights, moment of inertia, etc.):
See here - 3.
- Telescope Axis Motions:
The following specs are taken from here, which is the fundamental reference:- (a)
- Pointing Precision: 3 arcsec, rms radius
- (b)
- Tracking Precision: The drop-dead requirement is 165 mas per axis on time scales between 1 and 10 minutes. It is believed that the system can deliver 10 mas per axis in quiescent conditions, although this is not a requirement.
- (c)
- Maximum tracking rate:
- i.
- Azimuth: 45 arcsec/sec
- ii.
- Elevation: 15 arcsec/sec
- iii.
- Rotator: 45 arcsec/sec
- (d)
- Absolute position transducer precision:
- i.
- Altitude: 7.2 microns rms (
 microns at the transducer radius).
microns at the transducer radius).
- ii.
- Azimuth: 7.2 microns rms (
 microns at the transducer radius).
microns at the transducer radius).
- iii.
- Rotator: 30 microns rms (
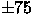 microns at the transducer radius).
microns at the transducer radius).
- (e)
- Normal operating range:
- i.
- Altitude: 25-87
- ii.
- Azimuth: 90
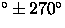
- iii.
- Rotator: 90
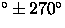
- (f)
- Normal velocity range: 0 to
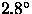 /sec, all axes.
/sec, all axes.
- (g)
- Maximum acceleration:
- i.
- Azimuth: 50
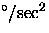
- ii.
- Altitude: 50
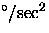
- iii.
- Rotator: 100
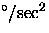
- (h)
- A specification on the motion of the secondary?
A.2 Basic parameters of the Photometric Telescope
These parameters describe the recently installed 20'' telescope from Johns Hopkins, and not the old 24'' Monitor Telescope, which has now been decommissioned.
- 1.
- Nominal optical design:
- (a)
- Primary mirror diameter: 500 mm
- (b)
- Primary mirror focal ratio: 3.00
- (c)
- Secondary mirror diameter: 200 mm
- (d)
- Nominal focal plane pixel scale (spectroscopic mode): 47.4 arcsec/mm
- (e)
- Focal plane radius 34.8 mm
A.3 Nighttime Operating conditions
- 1.
- Wind speed: <30 mph.
Basis: APO Operations shutdown limit - 2.
- Temperature: -20 to +20 C.
- 3.
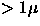 m dust counts below 3000, for at least 15 minutes. See
the
APO dust
policy.
m dust counts below 3000, for at least 15 minutes. See
the
APO dust
policy.
A.4 Basic parameters of imaging camera
The imaging camera was designed with the requirements of § 3 and § 4 in mind; see those sections for further details. See also the document, here.- 1.
- CCD active image area:
 pixels for photometric
chips, and
pixels for photometric
chips, and  pixels for astrometric and focus chips.
pixels for astrometric and focus chips.
- 2.
- Pixel size: 24 microns (0.4 arcsec).
- 3.
- Basic scan rate: 15 arcsec per sidereal second.
- 4.
- Number of CCDs:
- (a)
- Photometric: 30
- (b)
- Astrometric: 22 We could specify bridge and column chips separately.
- (c)
- Focus: 2
- 5.
- Transit time in drift scan mode:
- (a)
- Photometric CCDs: 55 sec
- (b)
- Astrometric and focus CCDs: 11 sec
- 6.
- The CCD should have the quantum efficiencies given by Table 8.2 of the Black Book.
- 7.
- Stars in astrometric chips 5.5 mags brighter in r' than star in photometric chips should have the same signal-to-noise ratio, in the brightness regime in which shot noise dominates the noise.
- 8.
- Stars in focus chips 2.5 mags brighter in r' than star in photometric chips should have the same signal-to-noise ratio.
- 9.
- The read noise of the chips should match the limits listed in Table 8.2 of the Black Book.
- 10.
- The dark current for the photometric chips should be no more than 6 electrons/pixel in 55 sec. For astrometric chips, no more than 60 electrons/pixel in 11 seconds.
- 11.
- The scatter in the pixel scale from chip to chip should be no more than 20% more than that in Table 6.2c (vscl).
- 12.
- The charge transfer efficiency (CTE) should be as listed in page 8.27 of the Black Book.
- 13.
- Center to center spacing of photometric CCD rows: 65 mm (17.98 arcmin)
- 14.
- Center to center spacing of photometric CCD columns: 91 mm (25.17 arcmin)
- 15.
- Overlap of scanlines within a stripe: 152 pixels (61 arcsec)
- 16.
- Overlap of scanlines between stripes: 402 pixels (161 arcsec)
- 17.
- Both astrometric and photometric chips should be rotationally
aligned to 0.25 pixel (5
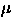 m). Tilt error
m). Tilt error 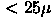 m, total
piston errors
m, total
piston errors 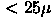 m.
m.
- 18.
- Temperature should be controlled to 1
 C;
temperature on astrometric bench should be uniform to
1
C;
temperature on astrometric bench should be uniform to
1 C.
C.
- 19.
- Focus should be controlled to 20
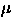 m rms at the secondary.
m rms at the secondary.
- 20.
- Filter effective wavelengths and widths:
- (a)
- u': 3540 Å, 570 Å
- (b)
- g': 4770 Å, 1370 Å
- (c)
- r': 6230 Å, 1370 Å
- (d)
- i': 7630 Å, 1530 Å
- (e)
- z': 9130 Å, 950 Å
- 21.
- Requirements on bias level, gain variations from chip to chip, and the full-well level of the chips?
A.5 Basic parameters of spectrographs
The spectrographs were designed with the requirements of § 7 in mind; see there for justifications and further details. See also the document here.- 1.
- Resolution: 1800-2000
- 2.
- The wavelength coverage should be continuous over the range 3900-9100 Å
- 3.
- Number of fibers: 640 (320 per spectrograph)
- 4.
- Fiber diameter: 180 microns
- 5.
- Wavelength coverage per channel:
- (a)
- Blue: 3900-6100 Å
- (b)
- Red: 5900-9100 Å
- 6.
- Pixel size:
- (a)
- Blue: 1.1 Å
- (b)
- Red: 1.6 Å
- 7.
- Resolution: 3 pixels
- 8.
- Spectrograph demagnification: 2.5
- 9.
- Fiber spacing at slit-head: 390 microns (156 microns or 6.5 pixels at CCD)
- 10.
- Dichroic crossover range: 200 Å
- 11.
- Plug-plate thickness: 3.2 mm
- 12.
- Plug-plate diameter: 813 mm
- 13.
- Focal plane radius: 327 mm
- 14.
- CCD read noise: 5 electrons rms per pixel
- 15.
- CCD full well: 300,000 electrons per pixel This may not be achievable
- 16.
- Ferrule diameter: 2.154 mm (plugging bit); 3.17 mm (total)
- 17.
- Minimum fiber separation: 55 arcsec due to the physical diameter of ferrule.
- 18.
- Light trap holes: 3.175 mm diameter
- 19.
- Size of central post: 47.625 mm diameter
A.6 Basic Parameters of Spectrograph Guide Camera
There is some controversy on the numbers below; we should find out the final numbers from Pat Waddell.- 1.
- Fiber diameter: 8 arcsec (9 bundles); 16 arcsec (1 bundle)
- 2.
- Scale: 60.6 arcsec/mm
- 3.
- Size:
 pixels (binned mode)
pixels (binned mode)
- 4.
- Pixel size: 18 microns
A.7 Data Acquisition System
- 1.
- Monitor Telescope (sdssmth)
- (a)
- Cpu: SGI Crimson R4400, 150 Mhz
- (b)
- Memory: 144 Mbytes
- (c)
- Disk:
 13 Gbytes
13 Gbytes
- (d)
- Tape drives: 2 DLT 2000
- 2.
- 2.5 M telescope (sdsshost)
- (a)
- Cpu: SGI Crimson R4400, 150 Mhz
- (b)
- Memory: 144 Mbytes
- (c)
- Disk:
 30 Gbytes
30 Gbytes
- (d)
- Tape drives: 2 DLT 2000
- 3.
- VME Crates: Spectroscopy and Photometric Telescope
- (a)
- Nodes (CPU boards): 2
- (b)
- Frame Pool (Spectro)
 50 frames
50 frames
- (c)
- Frame Pool (PT)
 ?? frames
?? frames
- (d)
- VCI+ boards: 3 (2 for spectro)
- 4.
- VME Crates: Imager
- (a)
- Number of crates: 3
- (b)
- Nodes (CPU boards): 10 (2
 3 for photometrics; 4 for astrometrics)
3 for photometrics; 4 for astrometrics)
- (c)
- Frame pool: 9 Gbytes per node
- (d)
- Capacity: 2.5 hours
- (e)
- Tape drives: 12 DLT 2000
- (f)
- Data rate to tape: 4.5 Mbytes/sec (total for photometrics).
- (g)
- Tape Capacity: Variable; 10-15 Gbytes (5 hours)
- (h)
- Cpu: 68040
- (i)
- Memory: 32 Mbytes per node
- (j)
- Frame Pool
 ?? frames
?? frames
- 5.
- Analysis Machine (sdss-commish)
- (a)
- CPU: Dual PPro 200 Mhz
- (b)
- Memory: 256 Mbyte
- (c)
- Disk: 44 Gbyte
A.8 What's Missing
This section does not describe specifications on all aspects of hardware. In particular:
- 1.
- We do not have complete information on fibers and plugplates.
- 2.
- We have only limited specs on the imaging camera CCDs, both photometric and astrometric.
- 3.
- We have nothing on the PT camera.
- 4.
- We have nothing on the production system at Fermilab (although this is covered somewhat in § 8).
Michael Strauss
8/5/1999